Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 47

47. Determine a resistência equivalente R a b no circuito da Figura 2.111 .

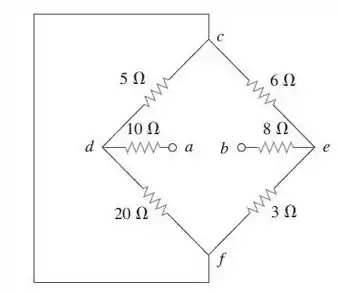
Passo 1

Bora lá resolver um probleminha sobre associação de resistores:

Vamos analisar esse caso, nomeando os nós com pontinhos destacados.

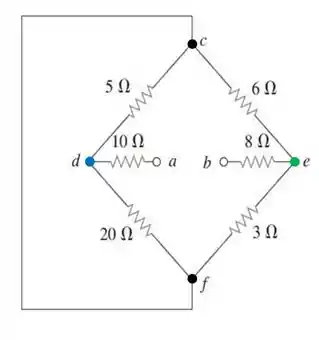
Vendo essa imagem, tiramos inicialmente que os nós c e f têm o mesmo potencial, portanto são iguais. Assim, temos que os resistores de 20   Ω e 5   Ω estão em paralelo. Calculemos a resistência equivalente para essa parte do circuito:

R e q 1 = ( 20 | | 5 )   Ω

R e q 1 = 20 ⋅ 5 20 + 5   Ω

R e q 1 = 4   Ω

As resistências de 6   Ω e 3   Ω também estão em paralelo. De modo que a resistência R e q 2 para essa parte do circuito é dada por:

R e q 2 = [ 6 | | 3 ]     Ω

R e q 2 = 6 ⋅ 3 6 + 3   Ω

R e q 2 = 2   Ω

Passo 2

Obtido assim o valor das resistências equivalentes das associações em paralelo, chegamos ao seguinte circuito:

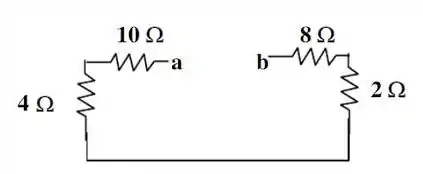
Todas essas resistências estão em série. Para obter a resistência R a b equivalente nos terminais a - b , basta somar esses valores:

R a b = 4 + 10 + 8 + 2   Ω

R a b = 24   Ω

Resposta

R a b = 24   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito da figura 2.90 , i 0 = 3 A . Calcule i x e a potência total dissipada pelo circuito.
Calcule I 0 no circuito da figura 2.91 .
Determine a R e q para o circuito da figura 2.94 .
Usando associações de resistências em série/paralelo, determine a resistência equivalente vista pela fonte no circuito da figura 2.98 e a potência total dissipada pela rede de resistores.
Determine R para o circuito da figura 2.101 .