Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 52
52. Para o circuito mostrado na Figura , determine a resistência equivalente. Todos os resistores são de .
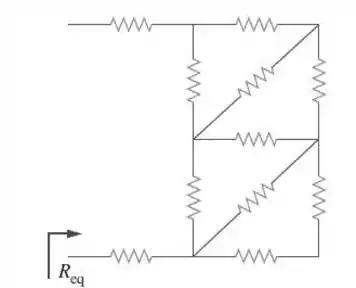
Passo 1
Bom! A primeira coisa que temos de fazer é destacar algumas partes importantes de nosso circuito! Vamos lá!
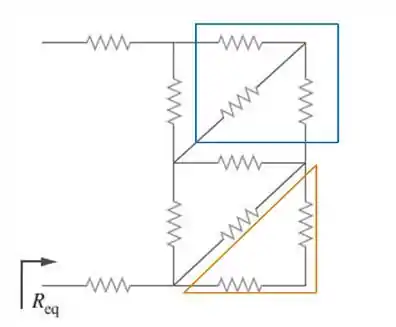
Essa parte alaranjada do nosso circuito tá bem fácil de entender! É uma conexão em série entre duas resistências de . A resistência equivalente portanto, vai valer . Só que essa resistência de está em paralelo com uma de , de modo que a nova resistência equivalente para esse trecho, , vai ser igual a:
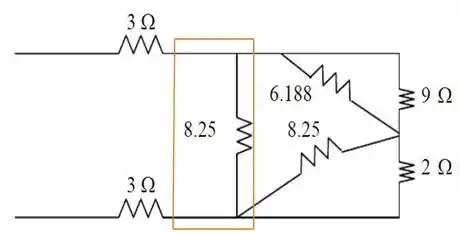
Já essa parte azul limitada por um quadrado, é uma conexão estrela , que não é a ideal para trabalharmos em nosso circuito. Por isso, façamos a transformação de para , esta sim mais apropriada.
Basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Onde temos que , o que nos leva ao seguinte resultado:
Mas não parou por aqui! Duas dessas resistências de vão estar em paralelo com resistências de , de modo que a resistência equivalente, , vai ser igual a:
Passo 2
E com isso, chegamos ao seguinte circuito:
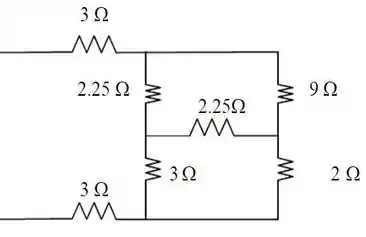
E novamente temos uma conexão estrela pela frente, como podemos ver na parte destacada em azul da figura, a seguir:
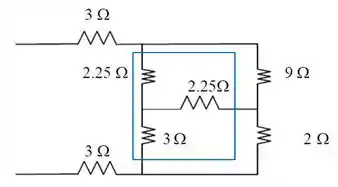
Temos que novamente, fazer a conversão de estrela para delta, onde:
Com isso, basta usar as equações a seguir, substituindo os valores correspondentes:
Passo 3
Obtido esses valores, o nosso circuito vai ficar com uma nova cara:
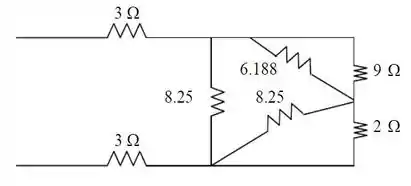
As resistências de e estão em paralelo. A resistência equivalente, , nesse caso é:
As resistências de e estão em paralelo. A resistência equivalente, , nesse caso é:
A soma dessas duas resistências anteriores, está em paralelo com essa resistência aqui de :
De modo, que a resistência equivalente, , para esse trecho vai valer:
Agora tuda está em série! Basta somar essa com as resistências de que sobraram, para obter a resistência total :