Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 50
50. Use a análise de malhas para determinar a corrente io no
circuito da Figura 3.95.
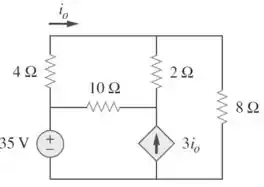
Passo 1
O exercício nos pede para usar a analise de laço, então devemos atribuir as correntes de malha, vamos dizer que a corrente da malha de cima da esquerda é , a corrente da malha da esquerda de baixo é e a corrente da malha da direita é .
Passo 2
Como esse circuito possui uma fonte de corrente precisamos definir uma supermalha em que a fonte de corrente esteja dentro. Ela vai ser formada pela malha da esquerda de baixo junto com a malha da direita. Agora vamos montar a equação interna da supermalha:
Então vamos aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) percorrendo a supermalha:
E só faltou aplicar a LKT na malha da esquerda de cima:
Dividindo por dois:
Passo 3
Agora é só resolver o sistema, podemos isolar o na equação menor e substitui-lo nas duas equações maiores:
Substituindo nas outras duas equações:
E então é só isolar o em alguma dessas equações e substituir na outra:
Substituindo: