Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 34
34-
Resolva o Problema 4.15 usando o método das correntes de malha.
Passo 1
Fallllaaaa meu queridoo!! Então, seguindo o que a questão nos pede, analisamos o circuito da questão 4.15 e vamos pra cima!!!
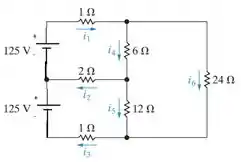
Utilizando o método das correntes de malha, temos:
−125 + 1i1 + 6(i1 − i6) + 2(i1 − i3) = 0
24i6 + 12(i6 − i3) + 6(i6 − i1) = 0
−125 + 2(i3 − i1) + 12(i3 − i6) + 1i3 = 0
Organizando as equações na forma padrão:
i1(1 + 6 + 2) + i3(−2) + i6(−6) = 125
i1(−6) + i3(−12) + i6(24 + 12 + 6) = 0
i1(−2) + i3(2 + 12 + 1) + i6(−12) = 125
Passo 2
Resolvendo as equações, temos:
i1 = 23,76 A;
i3 = 18,43 A;
i6 = 8,66 A
Calculando as correntes restantes:
i2 = i1 − i3 = 5,33 A
i4 = i1 − i6 = 15,10 A
i5 = i3 − i6 = 9,77 A
Passo 3
Pfontes = psuperior + pinferior = −(125)*(23,76) − (125)*(18,43) = −2969,58 – 2303,51 = −5273W
Conclui-se então que a nossa fonte forneceu 5273 W.
Agora calculando a potência consumida pelos resistores, temos:
p1superior = (23,76)2*(1) = 564,39W
p2 = (5,33)2*(2) = 56,79W
p1inferior = (18,43)2*(1) = 339,59W
p6 = (15,10)2*(6) = 1367,64W
p12 = (9,77)2*(12) = 1145,22W
p24 = (8,66)2*(24) = 1799,47W
Passo 4
A potencia total consumida pelos resistores:
564,39 + 56,79 + 339,59 + 1367,64 + 1145,22 + 1799,47 = 5273 W
Logo, a gente conclui que há um equilíbrio das potencias.
Resposta
5273 W.