Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 53
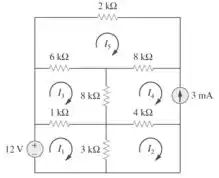
53. Determine as correntes de malha no circuito da Figura
3.98, usando o MATLAB..
Passo 1
O exercício nos pede para usar a analise de laço e ele já atribuiu as correntes de malha, então o primeiro passo da analise de malhas está feito.
Passo 2
Como esse circuito possui uma fonte de corrente onde só passa uma corrente de malha, sabemos que:
Então vamos começar a aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) nas malhas.
Malha 1:
Malha 2:
Nós já sabemos o valor de , então:
Malha 3:
Substituindo :
Malha 5:
Substituindo :
Passo 3
Agora que temos 4 equação e 4 incognitas podemos usar o MATLAB como o exercício pede para encontrar o valor das correntes:
Resposta
Exercícios de Livros Relacionados
Resolva o Prob. selecionando uma árvore apropriada e usando métodos da teoria de gráficos.
Use o método de conjunto de corte para resolver i no Prob. 6.4 .
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Selecione uma árvore apropriada e use o método desta seção para calcular i no circuito do exemplo 6.3 . 2 .
Mostre que (6.3) e valida nos circuitos do Problema 4.26,4.28 e 4.33.