Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 54

54- Determine o equivalente de Thévenin entre os terminais a - b do circuito da Figura 4.120 .

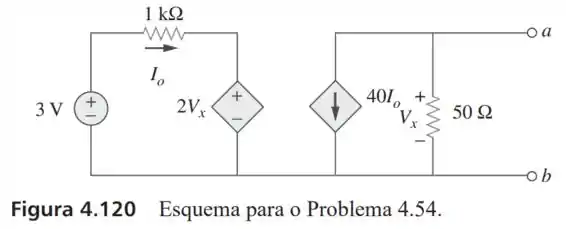
Passo 1

Note que pela malha direita temos que a tensão entre os terminais a e b valem:

V a b = V t h = V x

Agora precisamos encontrar equaçoes que correlacionam V x com I o , para isso temos as duas malhas.

Começando pela somatória de tensões na malha esquerda nós teremos:

3 - 1000 I o - 2 V x = 0 → 1000 I o + 2 V x = 3

Agora pela somatória das tensões na malha direita teremos:

V x - 40 I o × 50

Pois a corrente está contra o gradiente de V x (corrente indo do negativo para o positivo, enquanto deveria estar ao contrário). Dessa forma:

V x = - 2000 I o

Aplicando esse valor na primeira equação teremos:

1000 I o - 4000 I o = 3

I o = - 1   m A

Ou seja V x será:

V x = V t h = - 2000 × - 1   m A = 2   V

Passo 2

Pela resistência de 50   Ω influenciar diretamente na corrente de aumento do transistor então não podemos mais dizer que R t h valerá 50   Ω então para isso vamos fechar a conexão entre a e b para encontrarmos a corrente de Norton.

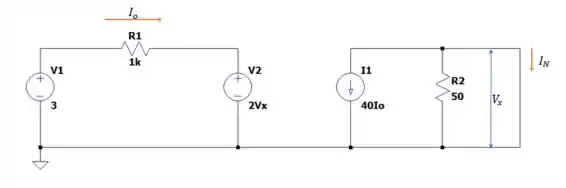
Por estarmos aterrando o terminal b e estarmos conectando b com a nós teremos que V x = 0 isso nos dará um I N (pela somatória das correntes na malha direita (igual a:

I N = - 40 I o

Pela malha esquerda nós podemos ver que não existe fonte de tensão dependente uma vez que 2 V x = 0 , logo a corrente I o será:

3 = 1000 I o

I o = 3   m A

Dessa forma a corrente de Norton será:

I N = - 40 × 3 m A = - 120   m A

Então a resistência de Thévenin será calculada como:

R t h = V t h I N = 2 - 120 m A = - 16.67   Ω

Mais um caso de resistência negativa (note que a fonte dependente na malha esquerda causa esse comportamento).

Resposta

V t h = 2   V

R t h = - 16.67   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

90- A ponte de Wheatstone mostrada na Figura 4.146 é usada para medir a resistência de um extensômetro (strain gauge). O resistor ajustável tem um ajuste linear com valor máximo igual a 100Ω . Se for
80- Use o Pspice ou MultiSim para determinar o circuito equivalente de Thévenin nos terminais a - b do circuito da Figura 4.125 .
85- O equivalente de Thévenin nos terminais a - b do circuito linear mostrado na Figura 4.142 deve ser determinado por meio de medições. Quando um resistor de 10k Ω é conectado aos terminais a - b , a
82- Uma bateria tem uma corrente de curto-circuito de 20A e uma tensão de circuito aberto de 12V . Se a bateria for conectada a uma lâmpada de resistência 2Ω , calcule a potência disspidada pela lâmpa
81- Para o circuito da Figura 4.126 , use o Pspice ou Multisim para determinar o equivalente de Thévenin nos terminais a - b .