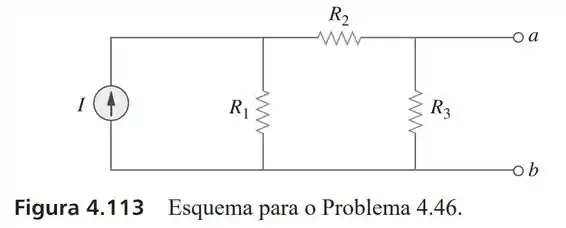
46- Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor circuitos equivalente de Norton.
Passo 1
Existem muitas formas de resolver essa questão, pois precisamos de valores de de , e e com isso vamos utilizar os dados da questão que nos dá:
Um problema clássico que quase todo exercício acaba cobrando de forma direta ou não é a de calcular a resistência equivalente de Norton do circuito entre os pontos e .

Vendo que as resitências e em série estão em paralelo com a resistência de tal modo que:
Passo 2
Outra coisa que podemos fazer é fechar os contatos e com a intenção de encontrar a corrente de Norton do circuito.
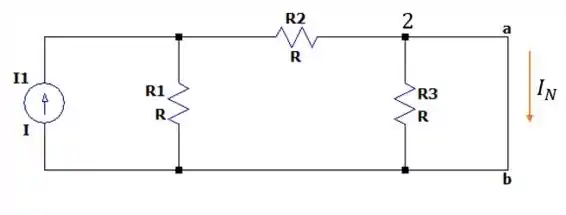
Como no nó nenhuma corrente passará pela resitência (pois os nós e estão curto circuitados) então teremos o seguinte circuito equivalente.

Onde:
Com a tensão em pode ser entendida da seguinte forma:
Onde é a corrente que passa por e a somatória dessas duas correntes vale:
Logo:
Substituindo tudo que conhecemos temos:
Isso nos dá:
Passo 3
E com essa informação podemos descobrir a fonte de tensão equivalente de Thevenin (que não é pedido mas é bom fazer para reforçar essa questão) a essa fonte de tensão que substitui a fonte de corrente do circuito.
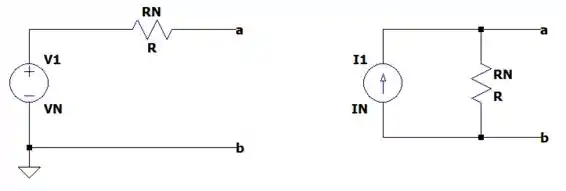
Dessa forma:
Como sabemos os valores de e temos a tensão: