Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 56
56. Determine no circuito da figura .
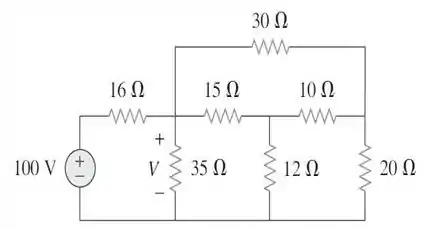
Passo 1
Bom! A primeira coisa que temos de fazer é destacar algumas partes importantes de nosso circuito! Vamos lá!
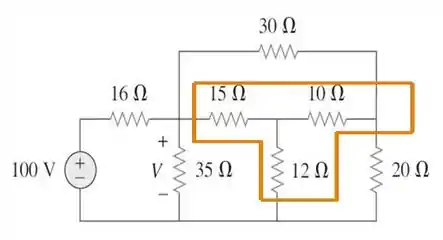
Essa parte alaranjada do nosso circuito tá bem fácil de entender! É uma conexão estrela , que não é a ideal para trabalharmos em nosso circuito. Por isso, façamos a transformação de para delta , esta sim mais apropriada.
Para fazer isso, basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Onde temos que:
O que nos leva ao seguinte resultado:
Passo 2
E com isso, chegamos ao seguinte circuito:
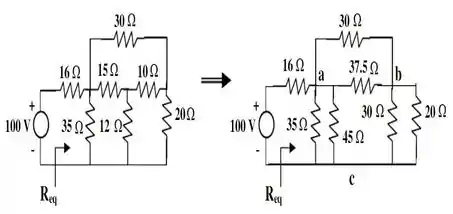
Dessa figura tiramos que os resistores de e estão dispostos em paralelo. De modo que a nossa resistência equivalente para esse caso é igual a:
Na figura podemos ver também que as resistências de e também estão em paralelo. Desse modo, a resistência dessa associação vai valer:
E o mesmo ocorre para as resistências de e ...
e estão em série. E o resultado desse associação está em paralelo com ... Assim, a resistência para essa parte do circuito vale:
Passo 3
Ótimo! Com esses dados, temos que o nosso circuito passa a ter a seguinte cara:
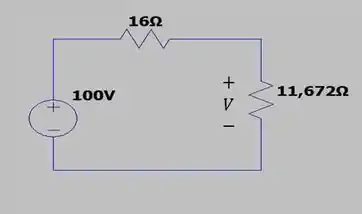
E para encontrar o valor de que é o que pede a questão, basta usar a divisão de tensão: