57. Determine e no circuito da Figura .

Passo 1
Bom! A primeira coisa que temos de fazer é destacar algumas partes importantes de nosso circuito! Vamos lá!
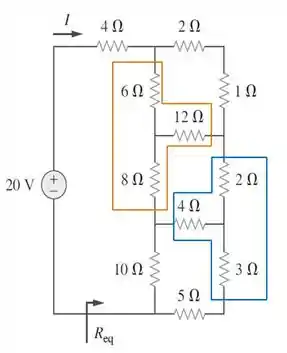
Repara só nas partes do circuito que estão envoltas pelas regiões alaranjada e azul! São conexões estrela, que não são o ideal para trabalharmos em nosso circuito. Por isso, façamos a transformação de para , esta sim mais apropriada.
Para fazer isso; basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Onde temos para a parte envolta pela região laranja:
E substituindo os valores correspondentes:
Obtemos o seguinte resultado:
Já para a parte envolta pela região azul, temos que:
E substituindo os valores correspondentes:
Obtemos o seguinte resultado:
Passo 2
Com esses resultados, chegamos ao seguinte circuito transformado:

Os pontos que estão com a mesma cor é porque tem o mesmo potencial. Repara que tem dois ramos do nosso circuito separados por pontos pretos e verdes. Eles contém as resistências de e , que estão em série e a resistência de E sabe o que quer dizer se eles estão separados por pontos da mesma cor?
Ora bolas! Quer dizer que esses resistores estão dispostos em paralelo. De modo que a nossa resistência equivalente para esse caso é igual a:
Na figura podemos ver também que as resistências de e estão em paralelo. Desse modo, a resistência dessa associação vai valer:
E o mesmo ocorre para as resistências de e ...
Passo 3
O nosso circuito então, vai ficar do seguinte jeito:
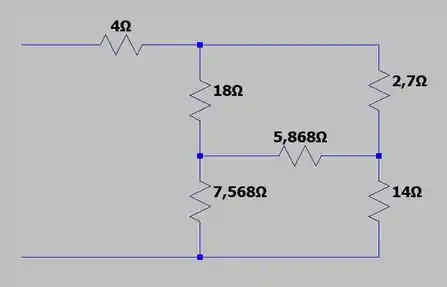
Agora repara só na parte que destacamos em vermelho:

Essa parte aí é uma configuração triangular, ou em delta, que não tá muito legal da gente trabalhar. Por isso, vamos fazer o caminho inverso ao que o gente vinha tomando e dessa vez fazer a transformação de delta para estrela:
Pra isso, basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Onde:
O que nos leva ao seguinte resultado:
Passo 4
E o circuito passa a ter a seguinte cara:
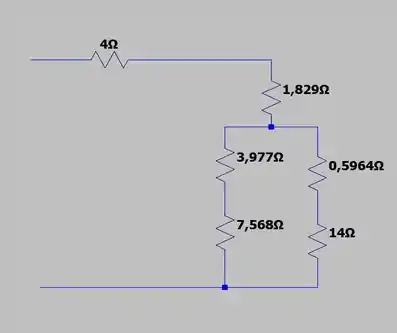
Onde percebemos que a resistência equivalente total é dada por:
Como a corrente é simplesmente a divisão da fonte de tensão de , pela resistência total equivalente , bora fazer o cálculo pra obter nosso resultado:
Pronto! Resposta encontrada!
Passo 5
Resposta
Ei, a resposta está no passo a passo :)