Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 59
59- Calcule a potência reativa no indutor e no capacitor da Figura
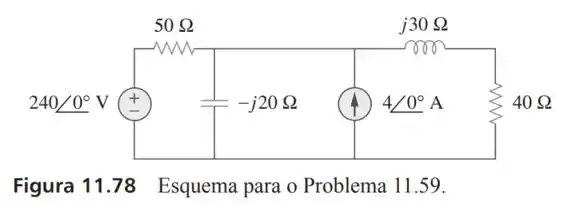
Passo 1
Vamos desenhar as correntes e as tensões que esse circuito possui.
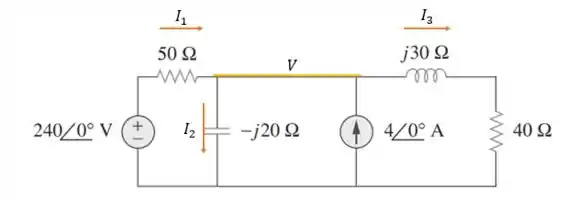
Note que toda a linha amarela no circuito tem a mesma tensão e vamos dizer que a tensão nessa linha vale então fazendo a somatória das correntes que entram e que saem dessa linha valem:
O que é a mesma coisa que:
Calculando :
Ufa.
Passo 2
Calculada a tensão nós podemos calcular a potência reativa no capacitor.
Agora para calcular a potência no indutor nós devemos encontrar a corrente .
Então a potência nesse indutor será:
Não precisa usar a fase da corrente e nem do circuito quando se eleva ao quadrado.
Resposta
Exercícios de Livros Relacionados
48- Determine a potência complexa para os seguintes casos: ( a ) P = 296W ,Q = 150V A R (capacitivo)
47- Para cada um dos casos a seguir, determine a potência complexa, a potência média e a potência reativa: d I = 10 ∠ 60AR M S ,Z = 100∠ 45 °Ω
48- Determine a potência complexa para os seguintes casos: ( b ) Q = 2000V A R ,F P = 0.9 (adiantado)
41- Obtenha o fator de potência para cada um dos circuitos da Figura 11.68 . Especifique se cada fator de potência está adiantado ou atrasado.
49- Determine a potência complexa para os seguintes casos: c ) V R M S = 208∠ 20 °V ,I R M S = 6.5∠ - 50°A