Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 58
58- Obtenha a potência complexa liberada para o resistor de da Figura a seguir.
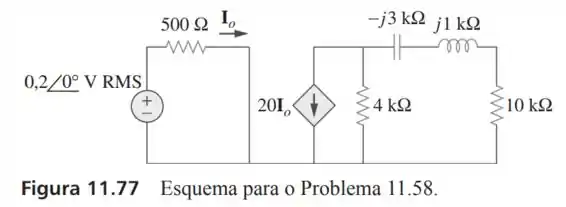
Passo 1
A análise não é muito diferente para a que foi feita em circuito de corrente contínua.
Pela malha esquerda nós conseguimos descobrir ao fazer.
Passo 2
Com isso temos que a fonte dependente libera uma corrente igual a:
Aí temos duas correntes que passam por essa malha, a corrente que passa pelo resistor de e a corrente que passa pela impedância equivalente de e vamos chamar de essa corrente de :
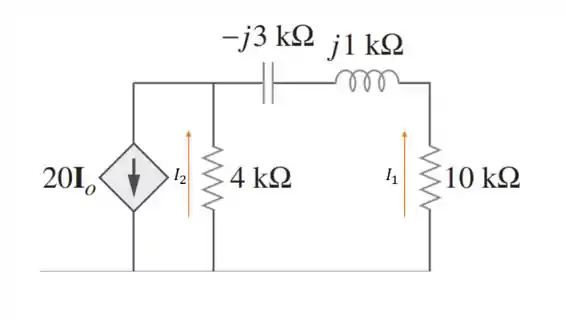
A corrente que passa por essa impedância equivalente será igual a:
Se tiver dúvida em como foi feito essa conta, dá uma revisada em corrente de circuito paralelo
Passo 3
Agora a potência total na resistência de será calculado por:
Resposta
Exercícios de Livros Relacionados
39- Um motor C A com impedância Z L = 4.2 + j 3.6Ω é alimentado por uma fonte de 220V ,60H z . ( a ) Determine F P ,P e Q . ( b ) Determine o capacitor necessário para ser conectado em paralelo com o
a) Se N 1 for igual a 1.000 espiras, quantas espiras deve ter o enrolamento N 2 do transformador ideal, no circuito apresentado na Figura P10.64, para que seja fornecida máxima potência média à carga
a) Determine a impedância de carga para o circuito da Figura P10.41 para a máxima transferência de potência média à carga, se ω = 8k r a d / s .b) Determine a máxima potência média fornecida à carga n
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de 240Ω em série com uma reatância indutiva de 70Ω ; a carga 2 é uma reatância capacitiva de
a) Determine as seis correntes de ramo I a - I f no circuito da Figura P10.36.b) Determine a potência complexa em cada ramo do circuito.c) Confirme seus cálculos verificando se a potência média fornec