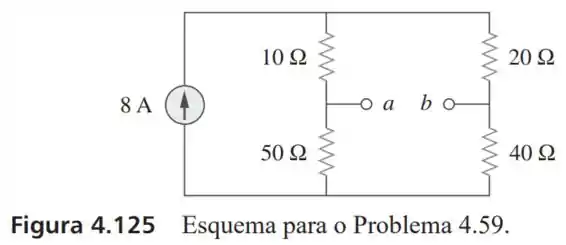
59- Determine os equivalentes de Thévenin e de Norton nos terminais a - b do circuito da Figura 4.125 .

R N = R t h = 22.5Ω V t h = 40V I N = 1.778A

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 59

59- Determine os equivalentes de Thévenin e de Norton nos terminais do circuito da Figura .

Passo 1

Não colocando nenhum aterramento nós teremos a seguinte malha de resistência.

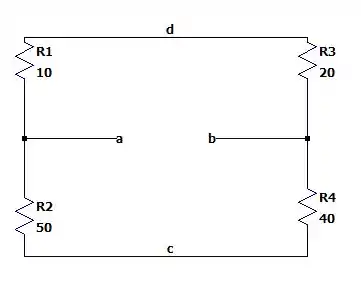
Onde a fonte de não terá nenhuma influência por estar conectada no vazio e para nos auxiliar desenhamos os nós e que nos abre a possibilidade de redesenhar essa malha da seguinte maneira.

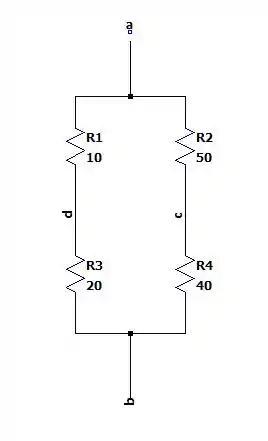
Fazendo a associação em paralelo encontramos a seguinte resistência de Norton.

Passo 2

Agora vamos tentar encontrar a diferença de potencial de e da seguinte forma:

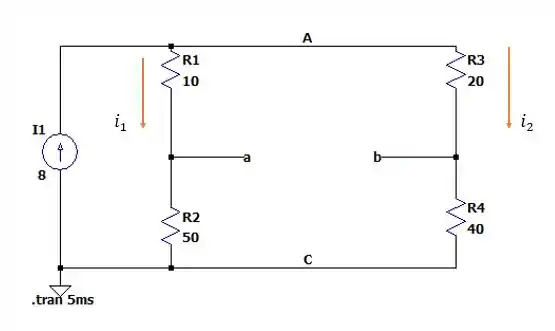
Onde a tensão de Thévenin será:

E pela figuraas duas correntes que estarão presentes nas duas linhas serão.

Dessa forma temos:

E por estarem ligados nos pontos e teremos a mesma tensão nas duas linhas e que será igual a:

Logo:

Então:

Logo:

Passo 3

Dessa forma para encontrarmos a corrente de Norton precisamos saber a relação entre Thévenin e Norton que é:

Logo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Através de transformações de fontes, substitua todo o circuito, exceto o resistor de 8Ω , por urn circuito equivalente com uma unica fonte e uma unica resistência R . Usando o resuItado, calcule v .

Converta todas as fontes na Figura do Ex. 4.2.3 para fontes de tensao e calcule v 3 :

Calcule a potência entregue a R quando (a) R=6Ω , (b) R=2Ω e (c) quando R recebe a potência máxima.

Mostre que as duas redes sao equivalentes, vistas pelos terminais a-b, e calcule a potência dissipada no resistor de 4Ω , em cada caso

Usando SPICE determine o circuito equivalente de Thévenin a esquerda dos terminais a-b. CaIcule o valor de R para a transferência máxima de potência e o valor da potência máxima...