Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 48
48- Determine o equivalente de Norton nos terminais para o circuito da Figura .
Passo 1
Para começar essa questão vamos interligar os nós e , pois se tentarmos calcular a corrente de Norton que passa sobre essa ligação infelizmente não encontraremos nada (meio que a fonte dependente de atrapalha nossa análise pois ela está ligada).
Quando temos essa situação o recomendado é interligar nessa conexão uma fonte de tensão ou de corrente unitária (isso é de ou ) no caso vamos conectar uma fonte de corrente de pois as variáveis na malha direita estão relacionadas com a corrente.
Isso nos dará a seguinte malha.
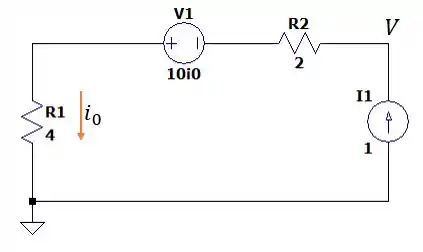
Supondo que a tensão em cima dessa fonte de corrente vale nós teremos então a seguinte somatória de correntes.
E consequentemente teremos a seguinte somatória de tensões nos componentes.
Pois numa fonte de tensão a fonte deveria fluir do sinal positivo para o sinal negativo e tanto na fonte de corrente quanto na fonte de tensão dependente a corrente de estão contra essa regra. Produzindo tensão negativa. Nos dando então uma tensão na fonte de corrente (‘’inventada’’) igual a:
Dessa forma a resitência que está entre os pontos e vale:
Essa resitência negativa é devida ao sinal da corrente colocado nessa conexão, mas ela faz sentido pois há uma fonte de tensão dependente que puxa essa corrente no sentido indicado. Esse é um tipo de fenômeno esquisito, mas se tratando de circuitos ativos isso pode acontecer.
Passo 2
No circuito equivalente de Norton somente precisamos da resistência e da corrente mas de vez em quando precisaremos da tensão de Thévenin para que a análise fique um pouco mais fácil.
Deixando o circuito aberto nos pontos e nós teremos que a fonte de corrente de despeja toda sua corrente na resistência de nos dando o seguinte circuito.
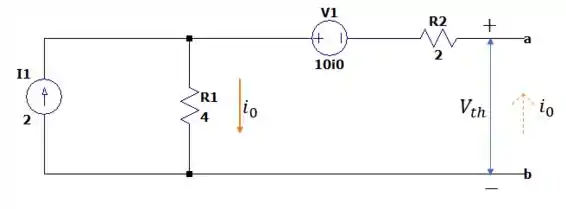
Sabendo que a tensão entre os pontos e valem então pela somatória das tensões na malha direita nós teremos:
Pois não flui nenhuma corrente no resistor de pois ele está conectada com que não está conectada em nada, logo não há diferença de potencial. Mas como existe corrente em então a fonte dependente está ligada. A tensão de Thevenin imagina-se que esteja ligada com corrente contra o gradiente de seus terminais.
Então a corrente de Norton entre vale: