Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 60
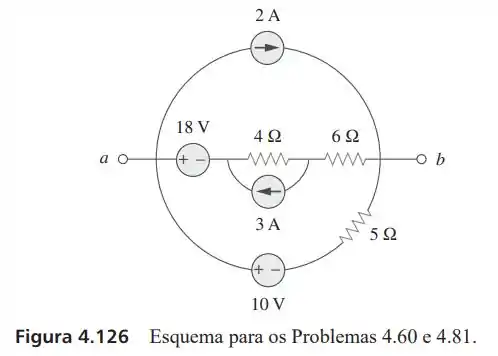
60- Para o circuito da Figura , encontre os circuitos equivalentes de Thévenin e de Norton nos terminais .
Passo 1
Com a bagagem que adquirimos das questões anteriores nós pudemos ser capazes de entender a transformar uma fonte de corrente para uma fonte de tensão e é isso que essa questão pede para nós fazermos.
Não o circuito todo de uma vez mas de pouco a pouco.
Vamos começar pela fonte de corrente de no meio desse círculo, se destacarmos ela nós teremos a seguinte fonte de tensão.
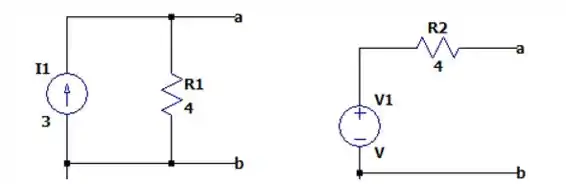
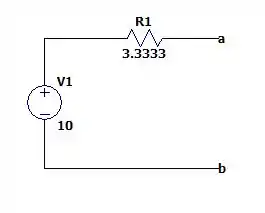
Para transformar essa fonte de corrente em uma fonte de tensão nós devemos desenhar ele dessa forma e com um valor igual a:
E a resistência dos dois circuitos são iguais.
O circuito fica da seguinte forma:
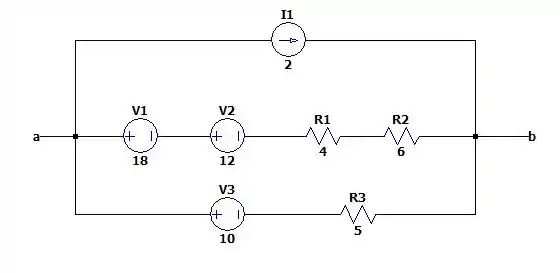
Somando as resistências e as fontes na linha intermediária acabamos por ter.
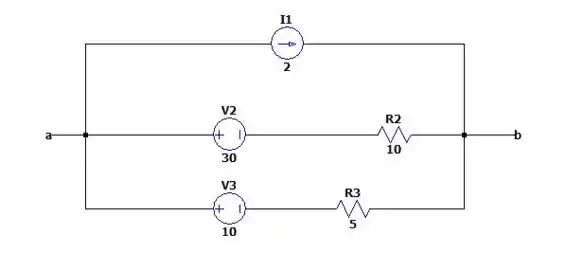
Passo 2
Agora vamos transformar a segunda linha e a terceira linha em fontes de corrente, para que possamos somar com a fonte de corrente que encontra acima de tudo.
Na segunda linha nós teremos uma fonte de corrente paralela a resitência de igual a:
E na segunda teremos uma fonte de corrente igual a:
Com o sentido apontando para o sinal positivo, da seguinte forma:
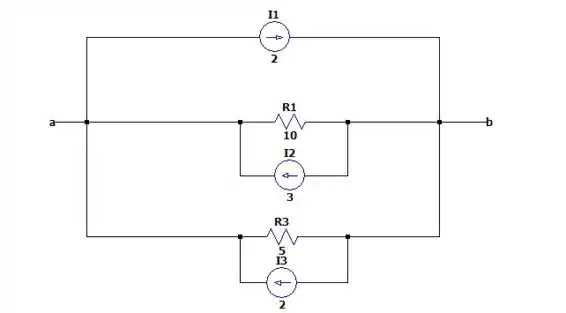
Somando todas as fontes de corrente nós teremos:
Com sentido indo de até e uma resistência equivalente igual a:
Isso é, nossa fonte de corrente (ou circuito de Norton ) será igual a:
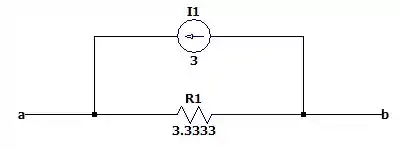
Passo 3
Já a nossa a forma de Thvenin ficaria com uma fonte de tensão igual a:
E seu circuito ficaria.
