Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 68
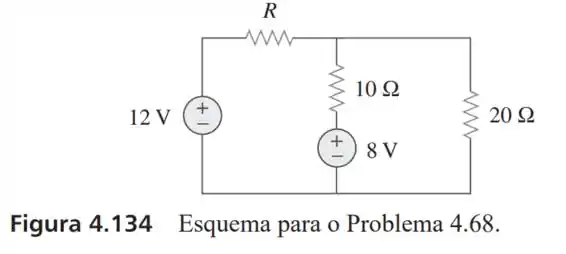
68- Calcule o valor de que resulta na máxima transferência de potência para o resistor de na Figura . Determine a potência máxima.
Passo 1
Nessa questão nós já temos a carga estabelecida então teremos que calcular a potência do jeito convencional ou seja:
Agora só teremos que nos preocupar em encontrar a maior corrente/ tensão que esse circuito pode gerar para a carga. Então vamos retirar a carga de e calcular a fonte equivalente.
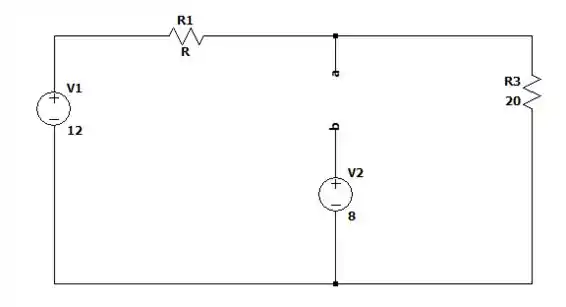
Vamos começar calculando tirando as fontes independentes .
Isso nos diz que as resistências de e de estão em paralelo, nos dando então um igual a:
Passo 2
Agora vamos calcular mas para isso vamos redesenhar o desenho de modo a conseguirmos ver algo mais interessante .
Isso pode ser escrito da seguinte forma:
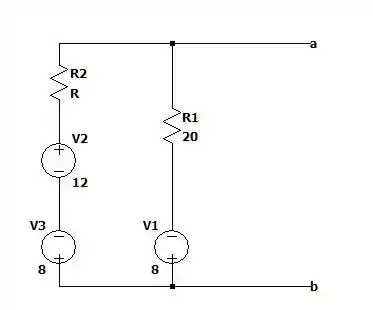
O que é:
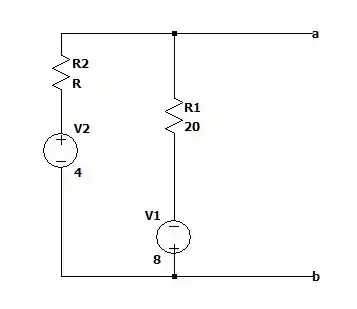
Agora transformando para duas fontes de corrente temos:
O que nos dá então uma fonte de corrente total igual a:
Logo a tensão de Thevenin valerá:
Passo 3
Dessa forma teremos a maior transferência de potência quando não existe para atrapalhar a corrente para essa carga (um valor de diminuirá o numerador e aumentará o denominador ou seja ele diminuirá e queremos que ele seja máximo para uma maior potência) :
Entenda como a tensão máxima que estará nos terminais ..
Para uma melhor visualização podemos plotar o gráfico da potência na resistência de .
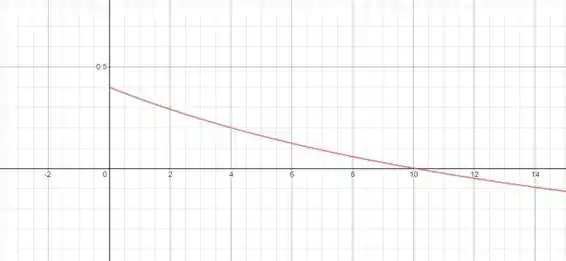
Assumindo que todo .
Note que do passo anterior encontrariamos para uma corrente de Norton igual a , ou seja é isso mesmo hahaha