Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 67
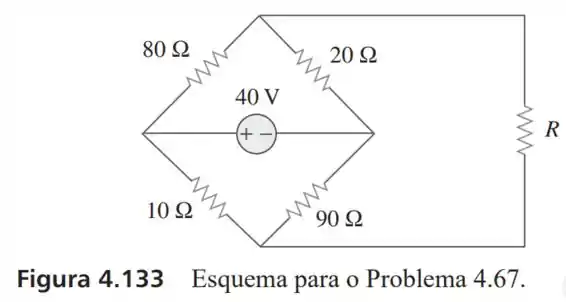
67- O resistor variável na figura é ajustado até absorver a potência máxima do circuito.
Calcule o valor de para a potência máxima
Determine a potência máxima absorvida por .
Passo 1
Vamos desaterrar o circuito e desconectar a fonte independente do circuito para calcular a resistência de Thevenin que enxerga.
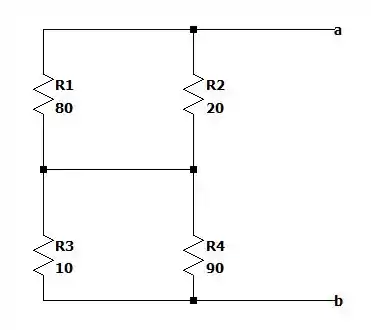
Dessa forma a resistência de e de estão em paralelo, assim como as resistências de e de também estão em paralelo. E essas resistências são iguais a:
O que nos dá uma malha resistiva equivalente igual a:
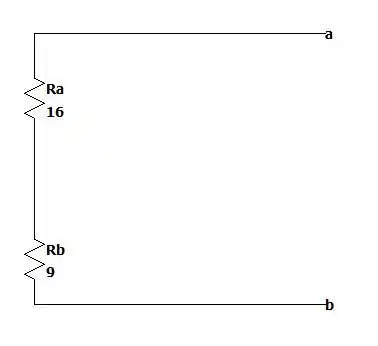
Dessa forma a resistência de Thevenin será:
E como vimos na seção 8 desse capítulo nós temos que a máxima potência se dá quando vale a resistência de Thevenin então essa é a resposta da letra a também.
Passo 2
Já para calcular a potência máxima nós precisamos calcular a tensão de Thevenin para podermos aplicar na fórmula abaixo.
Para isso vamos ver o circuito abaixo.
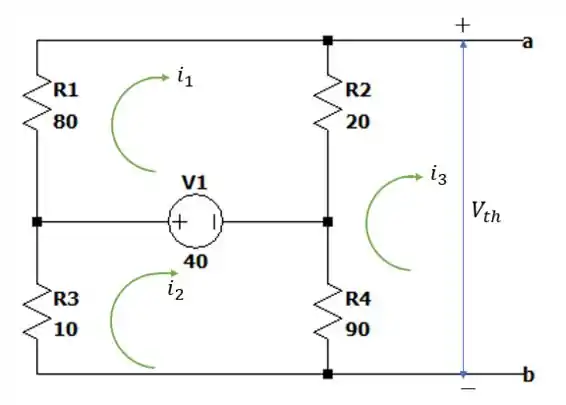
Onde é uma corrente imaginária que vamos utilizar somente para representar a somatória das tensões na malha onde ele se situa.
Fazendo a somatória das tensões na malha superior nós temos:
E a somatória das tensões na malha inferior será:
E a somatória das tensões imaginária na malha que sobra nos dá:
Passo 3
Então a potência máxima no resistor será de: