Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 72
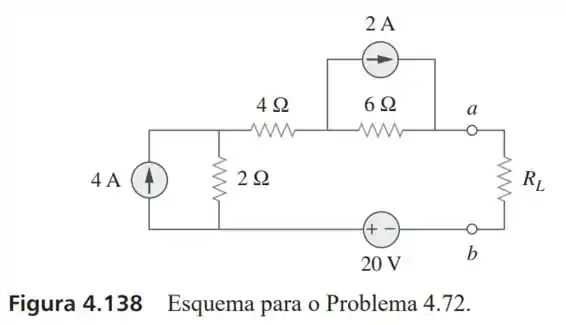
72- Para o circuito na Figura , obtenha o equivalente de Thévenin nos terminais .
Calcule a corrente em
Determine para a máxima potência que pode ser liberada para .
Determine essa potência máxima.
Passo 1
Fazendo a resistência de Thévenin nós conseguiremos responder a letra e metade da letra a (já que a máxima potência se dará quando ) .
Tirando todas as fontes independentes do circuito e tirando nós teremos a seguinte malha resistiva.
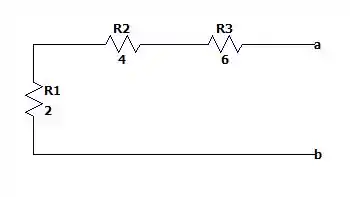
Isso é:
Passo 2
Já para encontrar a tensão de Thévenin vamos fazer o seguinte. Vamos transformar todas as fontes de corrente em fonte de tensão, nos deixando com o seguinte circuito.
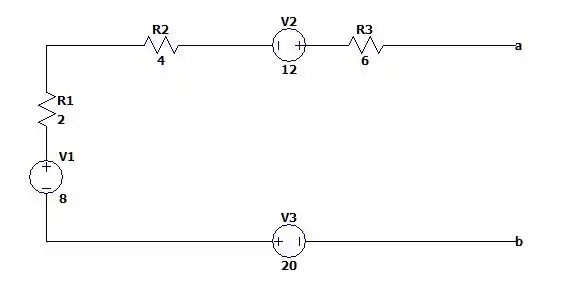
Somando as fontes de tensão e as resistências nós teremos o seguinte circuito de Thévenin.
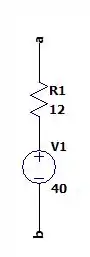
Dessa forma a tensão de Thévenin será:
Passo 3
Com teremos o seguinte circuito.
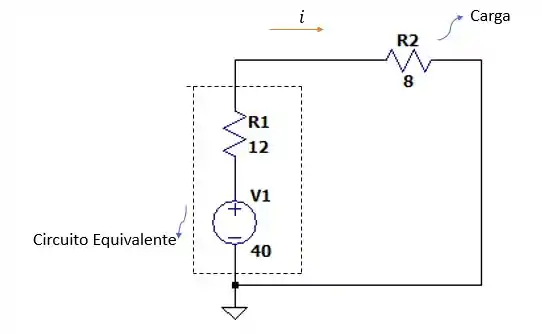
Então a corrente valerá:
Passo 4
Dessa forma a potência máxima será: