Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 98
98- Determine se o circuito com na Figura é estável.
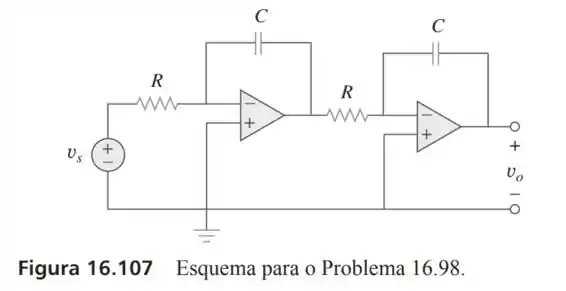
Passo 1
Como temos que a impedância de uma capacitor será:
Então a tensão da saída no primeiro amplificador inversor será de:
Passo 2
Agora a saída do segundo amplificador inversor será de:
Pelo que podemos ver na função de transferência os polos dessa função se darão em , e a princípio isso se configura em uma função marginalmente estável.
Passo 3
Agora transformando essa função de para nós teremos:
Fazendo vemos que a função tende ao infinito, então esse circuito é instável.
E se simularmos esse circuito vemos que independente dos valores de e de a saída sempre será o máximo de tensão que o amplificador pode fornecer.
Resposta
Circuito instável.
Exercícios de Livros Relacionados
Um pulso de tensão retangular, v i=[ u ( t )-u ( t-1 ) ]V , é aplicado ao circuito da Figura P13.59. Use a integral de convolução para determinar vo.
a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vi para o circuito na Figura P13.51.b) Determine o valor numérico de cada polo e zero de H(s).
a) Determine a função de transferência Io/I g como uma função de μ , para o circuito da Figura P13.57. b) Determine o maior valor de m que produzirá um sinal de saída limitado para um sinal de entrada
Determine a expressão numérica para a função de transferência (Vo/Vi ) de cada circuito da Figura P13.52 e os valores numéricos dos polos e zeros de cada função de transferência. Determine a expressão