Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 102

102- Sintetize a função de transferência

V o s V e n t s = 10 6 s 2 + 100 s + 10 6

Usando a topologia da Figura 16.111 . Seja Y 1 = 1 / R 1 , Y 2 = 1 / R 2 , Y 3 = s C 1 , Y 4 = s C 2 . Adote R 1 = 1 k Ω e determine C 1 , C 2 e R 2 .

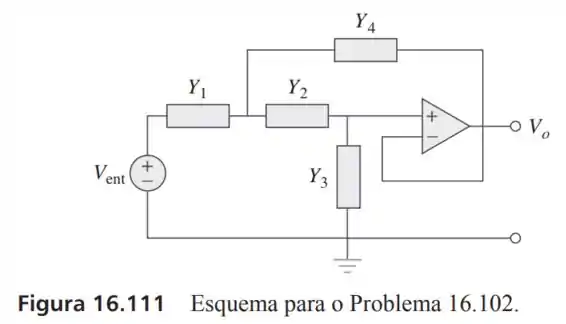
Passo 1

Vamos desenhar o circuito com o seguidor de tensão e descobrir função de transferência com as susceptâncias dadas na questão:

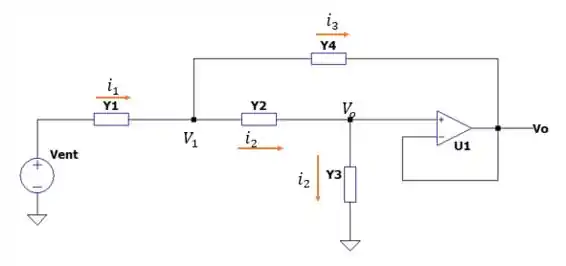
Uma vez que a tensão na porta não inversora é a mesma que na porta inversora e vale V o , e nenhuma corrente entra nas portas de entrado do A O P .

E outra coisa que precisamos saber é como calcular a corrente com a susceptância, imagine que temos uma corrente i 1 atravessando R 1 e não Y 1 normalmente calcularíamos a corrente assim:

i 1 = V e n t - V 1 R 1

Só que como Y 1 = 1 R 1 então:

i 1 = V e n t - V 1 Y 1

Calculando as correntes que entram e saem em V 1 nós temos:

i 1 = i 2 + i 3

V e n t - V 1 Y 1 = V 1 - V o Y 4 + V 1 - V o Y 2

V e n t Y 1 = V 1 Y 1 + Y 4 + Y 2 - V o ( Y 4 + Y 2 )

Só que:

V 1 - V o Y 2 = V o Y 3

V 1 = V o Y 2 + Y 3 Y 2

Substituindo na primeira equação:

V e n t Y 1 = V o Y 2 + Y 3 Y 2 Y 1 + Y 4 + Y 2 - V o ( Y 4 + Y 2 )

V e n t V o = Y 2 + Y 3 Y 1 + Y 2 + Y 4 Y 1 Y 2 - ( Y 4 + Y 2 ) Y 1

V o V e n t = Y 1 Y 2 Y 2 + Y 3 Y 1 + Y 2 + Y 4 - Y 2 ( Y 4 + Y 2 )

V o V e n t = Y 1 Y 2 Y 1 Y 2 + Y 1 Y 3 + Y 2 Y 3 + Y 3 Y 4

Passo 2

Como Y 1 = 1 / R 1 , Y 2 = 1 / R 2 , Y 3 = s C 1 , Y 4 = s C 2 :

Então:

V o V e n t = 1 R 1 R 2 1 R 1 R 2 + s C 1 R 1 + s C 1 R 2 + s 2 C 1 C 2

Dividindo tudo por C 1 C 2 para termos o mesmo esquema da função de transferência dada no enunciado nós temos:

V o V e n t = 1 R 1 R 2 C 1 C 2 s 2 + 1 R 1 C 2 + 1 R 2 C 2 s   + 1 R 1 R 2 C 1 C 2

Então:

1 R 1 R 2 C 1 C 2 = 10 6

1 R 1 C 2 + 1 R 2 C 2 = 1 C 2 R 2 + R 1 R 2 R 1 = 100

Onde:

R 1 = 1   k Ω

Com duas equações para três incógnitas vamos supor mais um valor, tal como R 2 = 5   k Ω , isso nos dá:

1 C 2 6 k 5 M = 100 → C 2 = 12   μ F

C 1 = 1 10 6 × 5 k × 1 k × 12 μ = 16.67   n F

Resposta

R 2 = 5   k Ω ; C 1 = 16.67   n F ; C 2 = 12   μ F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o circuito da Figura 7.110. Determine i ( t ) para t 0 e t0 .
Calcule a tensão no capacitor para t0 e t0 para cada um dos circuitos da Figura 7.106.
Para o circuito na Figura 7.113, i_s ( t ) = 5 u ( t ) . Determine v ( t ) .
Determine v ( t ) e i ( t ) no circuito da Figura 7.115.
Determine v ( t ) para t0 no circuito da Figura 7.114 se v (0) = 0 .