Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 1
O amp op no circuito da Figura P5.1 é ideal.
a) Identifique os cinco terminais do amp op com seus respectivos nomes.
b) Qual restrição do amp op ideal determina o valor de in ? Qual é esse valor?
c) Qual restrição do amp op ideal determina o valor de ( v p - v n )? Qual é esse valor?
d) Calcule v o .
Passo 1
Vamos escrever as entradas direto no circuito: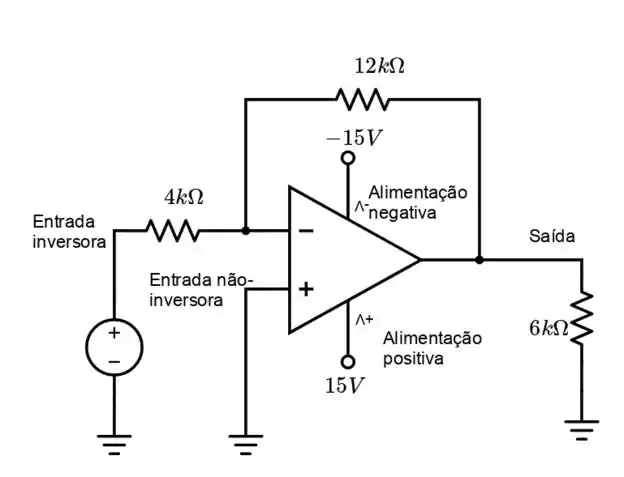
Passo 2
Na teoria de circuitos, o amplificador operacional ideal tem a impedância ou resistência de entrada infinita, assim a corrente de entrada é 0.
Passo 3
A diferença entre e deve ser zero, porque o ganho de malha aberta do amplificador operacional ideal é infinita, assim a diferença é zero. Isso também é chamado de aterramento virtual :)
Passo 4
Vamos escrever a equação na malha de entrada do circuito:
Como sabemos que tanto como são 0, podemos tirá-los da equação:
Isolando :
Resposta
a) No desenho
b)
c)
d)