Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 11
Aplique a análise nodal ao circuito da Figura 10.60 e determine .
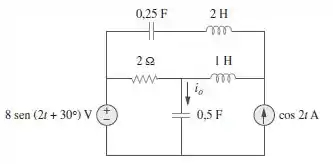
Passo 1
Vamos lá! A questão nos pede para resolver por análise nodal, mas antes vamos levar todo mundo para o domínio da frequência. De tal modo que,
Agora que levamos para o domínio da frequência vamos encontrar as equação para cada nó.
Passo 2
Note que, para o nó 1
Para o nó 2,
Multiplicando a primeira por 4, temos
Somando as duas equações,
Como ele pede a corrente , temos que
Logo,
Resposta
Exercícios de Livros Relacionados
Use o método das tensões de nó para determinar V 0 no circuito da Figura P9.54
Use o método das tensões de nó para determinar Vo e Io no circuito da Figura P9.59.
Use o método das correntes de malha para determinar a expressão de regime permanente para vo no circuito da Figura P9.64, se vg for igual a 75 cos 5.000t V.
Use o método das tensões de nó para determinar o fasor tensão Vo no circuito da Figura P9.58. Expresse a tensão nas formas polar e retangular.
A fonte de tensão senoidal no circuito mostrado na Figura P9.69 está gerando a tensão vg = 20 cos 5.000t V. Se o amp op for ideal, qual será a expressão de regime permanente para vo(t)?