Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 12a
Calcula da equação diferencial e use o resultado para calcular a resposta forçada para para uma tensão de entrada de .
Passo 1
Faaaala meu povo!! Como vocês estão? Bora lá resolver mais uma questãozinha?
O primeiro passo compreende em redefinir o diagrama, aplicando a tensão de entrada e escrevendo os números complexos na forma angular.
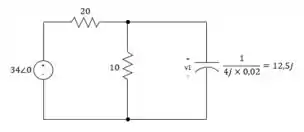
Passo 2
Considerando o passo anterior, faremos o cálculo da Resistência equivalente ():
Passo 3
Agora forçaremos a resposta para :
Então é isso pessoal! Bons estudos e até a próxima...
Resposta
Exercícios de Livros Relacionados
Mostre que, se i e uma senoide amortecida, i = I m e σ t cos ( w t + ϕ ) Então v , definido por v = L d i d t + R i É também uma senoide amortecida de mesma frequência complexa.
Calcule as frequências naturais do circuito do Ex. 14.4.2 matando a fonte e usando (a) uma entrada de alicate em serie com 0 capacitor e (b) uma entrada de soldagem através do capacitor. (Nota: não ca
Calcule as frequências naturais do circuito da Fig. 14.5 matando as fontes e usando (a) uma entrada de alicate em serie com 0 capacitor e (b) uma entrada de soldagem através do capacitor.
Um filtro passa-todas é o filtro cuja resposta em amplitude e constante. (Então, ele passa todas as frequências igualmente bem). Pode ser Iigado em cascata com outro filtro par manter uma resposta em
Para o circuito RLC paralelo em ressonância, mostre que a energia total armazenada é w t = 1 2 R 2 C I M 2 cos 2 w 0 t + R 2 I M 2 2 w 0 2 L sin 2 w 0 L = 1 2 R 2 C I M 2 Onde a excitação é i = I