Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.2 - Ex. 4

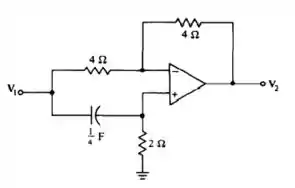
Um filtro passa-todas é o filtro cuja resposta em amplitude e constante. (Então, ele passa todas as frequências igualmente bem). Pode ser Iigado em cascata com outro filtro par manter uma resposta em amplitude desejada, mas altera a fase. Mostre, por meio da função de rede , a resposta em amplitude e a resposta em fase, que 0 circuito dado e um filtro passa-todas de primeira ordem.

Passo 1

Nessa questão um filtro passa-todas é o filtro cuja resposta em amplitude e constante. (Então, ele passa todas as frequências igualmente bem). Pode ser Iigado em cascata com outro filtro par manter uma resposta em amplitude desejada, mas altera a fase. Mostre, por meio da função de rede , a resposta em amplitude e a resposta em fase, que 0 circuito dado e um filtro passa-todas de primeira ordem.

Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.

Passo 2

Sabendo que,

A função de rede vale para,

Sendo para resposta de fase

Ficando,

Resposta

Exercícios de Livros Relacionados

Para o circuito mostrado, R = 2 Ω , L = 2 H e C = 0.02F . Se a entrada e a saida forem V 1 e V 2 , respectivamente, calcule a funçāo de rede e esboce as respostas em amplitude e fase. Mostre que o pic

Calcule H ( s ) = V 2 ( s ) / V 1 ( s ) e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem e m ω = 4 r a d / s .

Se R 1 = R 2 = 0,5 Ω e R 3 = 0,01 Ω no Prob. 15.4 , calcule H ( s ) . a frequência ω n na qual o pico da amplitude e a fase zero ocorrem e o módulo de H em ω 0

Altere em escala o circuito do Prob. 15.32 para obter um filtro passa-altas com ω t = 2000 r a d / s , usando capacitores de 0,05 μ F .

Mostre que, no caso geral, o circuito do Prob. 15.4 é um filtro passa-faixa com freqüência central 1 / R 3 r a d / s , largura da faixa 1 / R 2 r a d / s , ganho R 2 / R 1 e índice de mérito R 2 / R 3