Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 14
Se , calcule , , , e em e em .
Passo 1
Iae, meus queridos! Td blzinha? Essa questão é bem parecida com a anterior 7.13, então vamos tirar de letra.
Vamos analisar o circuito no instante primeiramente.
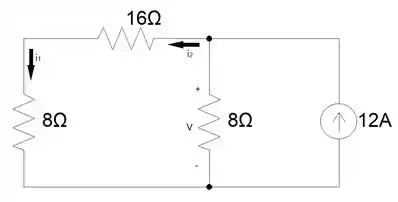
o enunciado da questão já nos deu, . Observamos também que obrigatoriamente , aplicando Lei de Ohm no resistor de da direita do circuito, podemos encontrar a corrente que passa por ele e, por analise nodal, encontrar e .
Portanto, se toda corrente que entra em um nó é a mesma que sai, .
Não esquecemos do capacitor, por ele estar completamente carregado nesse instante sua corrente . Já sua tensão será a mesma tensão que age sobre o resistor de da esquerda do circuito, então basta aplicarmos a Lei de Ohm nele que brota no rolé. 😉
Moleza né?
Passo 2
Para o instante
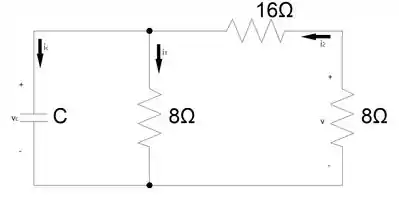
Vimos que , isso implica que e com isso podemos calcular aplicando a lei que rege os engenheiros eletricistas... a Lei de Ohm!
Rapidamente calculamos a resistência equivalente da associação em série e somando-as, logo depois aplicando a Lei de Ohm e calcular .
Nesse instante é a corrente que passa pelo resistor de da direita do circuito, então podemos calcular .
Por fim, para calcular , aplicamos analise nodal e somamos as correntes e , portanto.
Eu disse que íamos tirar de letra. 😎
Resposta
.
.
.
.
.