Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 17
As capacitâncias mostradas são todas em uF. Calcule a capacidade equivalente vista pelos terminais a-b.
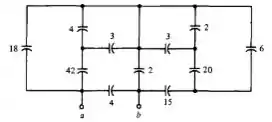
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar a capacitância equivalente. Vai ser tranquilo. Partiu??
Ok, agora o nosso problema vai ser relembrar qual a fórmula de um capacitor em série e em paralelo. Responde Aí!! Lembrou?? Não?!
Vamos usar a associação em paralelo como:
E para a associação em série.
Passo 2
Então bora láa!! Vamos analisar esse circuito.
Primeira coisa vamos nomear os pontos. Assim, temos que
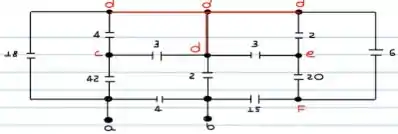
Pronto!!
Agora, partindo do terminal para o terminal, vamos ter o seguinte circuito
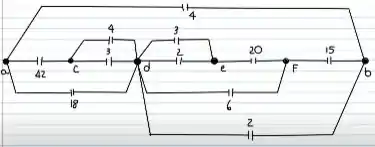
O segredo aqui é começar por dentro do circuito. Então entre C e D, temos dois capacitores em paralelo.
Assim, pela fórmula, resultará em:
O circuito resultante será:
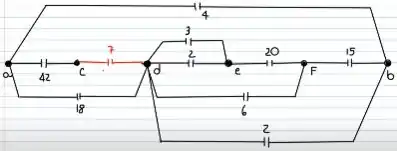
Agora, temos dois capacitores em série entre A e D. Pela fórmula:
O circuito resultante será:
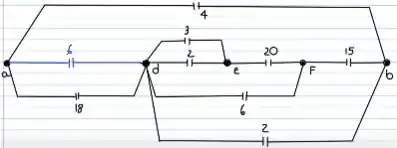
Entre A e D, temos dois capacitores em paralelo. Pela fórmula:
O circuito resultante será:
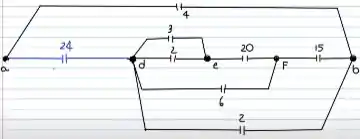
Entre D e E, temos dois capacitores em paralelo. Pela fórmula:
Continuando, já temos entre D e F dois capacitores em série. Pela fórmula:
O circuito resultante será:
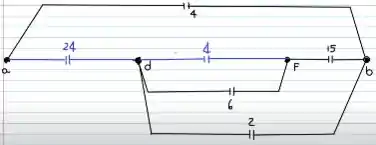
Está cansado?? Aguenta aí que estamos quase acabando!!
Passo 3
Agora vamos para o último passo!!
Entre D e F, temos dois capacitores em paralelo. Pela fórmula:
Continuando, já temos entre D e B dois capacitores em série. Pela fórmula:
O circuito resultante será:
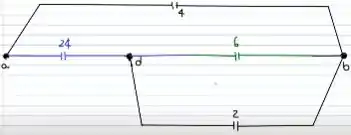
Entre D e B, temos dois capacitores em paralelo. Pela fórmula:
Continuando, já temos entre A e B dois capacitores em série. Pela fórmula:
O circuito resultante será:
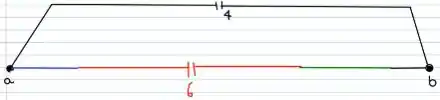
Finalizando então!!!!
Entre A e B, temos dois capacitores em paralelo. Pela fórmula:
Pronto!!