Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 5
Calcule e para se = 1A
Passo 1
Vamos arrebentar em mais uma questão de RC?!
A questão pede pra descobrirmos a tensão que está passando no resistor de 24Ω e corrente do resistor de 2Ω.
Vamos primeiro analisar nosso circuito.
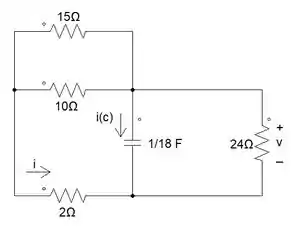
Vamos ter que fazer a associação de todos os resistores para acharmos um . Vamos lá!
O resistor de 15Ω está em paralelo com o de 10Ω.
//
//
//
O resistor de está em série com o de .
= 6 + 2
= 8Ω
Assim, fica nosso circuito:
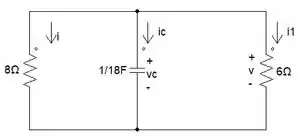
Antes de terminarmos a associação dos resistores, vamos estabelecer algumas relações.
; ;
Agora, sim, vamos concluir essa associação!
O resistor de 8Ω está em paralelo com o de 24Ω.
//
//
//
Passo 2
Tá mandando bem dmsss! Dá só uma olhadinha como ficou nosso circuito equivalente.
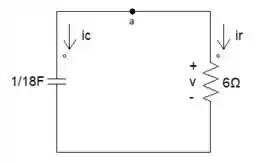
Depois de acharmos nosso circuito equivalente, vamos achar o .
Facinho né?! Feito isso, vamos utilizar o valor do na equação para descobrirmos a constante A.
Mas, peraí! Não sabemos a tensão ainda. Calma! Lembra quando definimos o valor de lá no Passo 1? Vamos usar a lei de Ohm, assim, acharemos nossa tensão.
Maravilha! Sabendo a tensão, ficou tudo mais fácil! Então, vamos lá! Substituindo na equação, teremos:
Tá mandando ver!! Muito bem 😉. Agora, só vamos substituir todos os valores na equação e obter nosso final.
Passo 3
Sensacional! Estamos quase terminando. Falta pouquinho agora. Só precisamos achar agora, a equação do . Para isso, vamos usar uma velha amiga nossa: a lei de Ohm.