Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 27
Calcule para , se o circuito está em regime permanente em .
Passo 1
Fala, pessoal. Tudo tranquilo? Vocês estão mandando muito nas questões. Mas, vamos continuar praticando. Olha só esse circuito RC, a questão nos pede a tensão do capacitor de . Vamos fazer juntinhos e arrasar! 💪
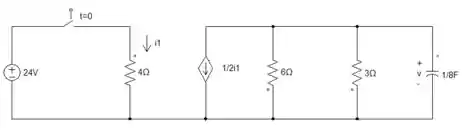
Para essa questão, teremos que fazer a análise em regime permanente e em regime transitório, então vamos começar pelo permanente. Partiu 😎
Vamos ver como fica nosso circuito em regime permanente.
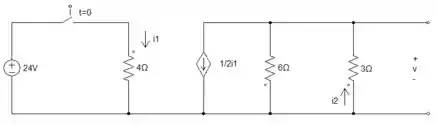
Nessa parte, nossa chave irá se abrir e se o circuito fica em aberto nessa parte, não terá corrente passando. Logo, a fonte de corrente dependente não terá corrente para ser transmitida pelo circuito e a tensão
Tudo entendido? Fácil essa primeira parte né?
Passo 2
Muito bom! Vamos partir agora para o regime transitório para encontrar nosso . Vamos lá, pessoal! Olha só como vai ficar nosso circuito agora:
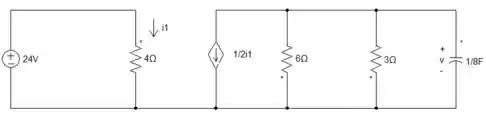
Quando o regime for transitório, a chave irá fechar e aí sim teremos corrente circulando no circuito.
Como a fonte dependente é então a segunda fonte de corrente vale:
Passo 3
Maravilha! Agora ficou mais fácil né? Reparou que temos dois resistores em paralelo? Vamos fazer essa associação?!
//
//
//
Vamos ver como ficou essa parte do circuito agora?
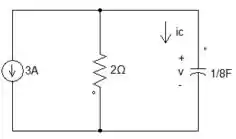
Belezinha! Agora, precisamos fazer LKT na 1ª malha para chegarmos a EDO do circuito. Vamos lá!
Malha 1:
Putz! E agora??? 😲 Ixiii...vamos ter que usar a função logarítmica. Mas, fica tranquilo, vamos te mostrar como é de boa. Partiu?
Passo 4
Ufaaa! Finalmente, achamos nossa expressão para o , mas peraí, não sabemos quanto vale a constante C. Para isso, vamos pegar o valor da tensão quando está em regime permanente
Belezinha, pessoal. Essa parte foi bem tranquila né? Ei, estamos quase terminando, só vamos achar agora o e o Para o vamos usar:
Blz! Vamos substituir os valores que já temos
Muito bem! Tirou onda! Parabéns!!!