Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 3
(a) Determine e a energia inicial (t=0), no circuito série, se e =. (b) Calcule a porcentagem da energia inicial, que é dissipada no resistor para t > 100ms.
Passo 1
Iae, pessoal!!
Partiu tirar onda nessa questão de circuito RC? Essa questão é bem tranquila. Ela nos pede o valor do e do e a porcentagem da energia inicial para t > 100ms.
Tendo isso em mente, vamos dar uma olhadinha no nosso circuito.
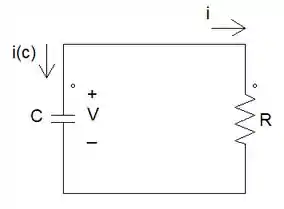
No enunciado nos foi dado o valor da tensão e da corrente e isso nos lembra a lei de Ohm. Vamos utilizá-la para descobrirmos o valor de
Para acharmos o , vamos usar a fórmula do τ. Na expressão do e do , ele nos diz que τ =1/5. Então, vamos lá!
Passo 2
Tá mandando muito bem! Vamos continuar metendo bronca. Agora, vamos descobrir quanto vale a energia inicial desse circuito. Vejamos, a fórmula da energia é dada por:
. Depois de descobrirmos quanto vale o capacitor, vamos substituir na equação junto com o valor de que foi dado na questão.
J
Passo 3
Muito bem! Estamos quase acabando, só precisamos achar a porcentagem da energia inicial quando t > 100ms. Por definição, a constante de tempo é o tempo necessário para que a tensão caia 36,8% da sua tensão inicial, assim, a porcentagem é dada por 36,8%.
Resposta
a); ; J
b)36,8%.