Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 24
Calcule i para t > 0, se i(0) = 5 A.
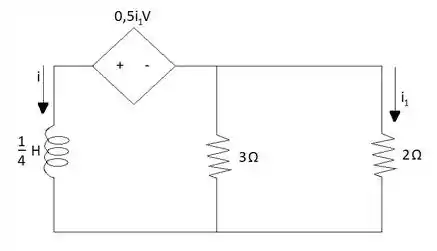
Passo 1
Olá pessoal, temos mais uma questão a ser resolvida, espero poder ajudar vocês com ela, vamos lá.
Essa questão aparenta ser muito simples de ser resolvida, mas é preciso ter sempre cuidado no momento de resolver. Ela pede a expressão da corrente i no decorrer do tempo sendo que a fonte de tensão é dependente do valor de uma corrente no circuito, sendo assim, precisamos encontrar o valor dessa corrente ou uma relação entre os valores das correntes dadas, já que como estão no mesmo circuito elas podem se relacionar.
Antes de começar a resolução do problema é necessário levar em consideração os polos positivo e negativo de cada elemento do circuito, que por análise se tem o seguinte:
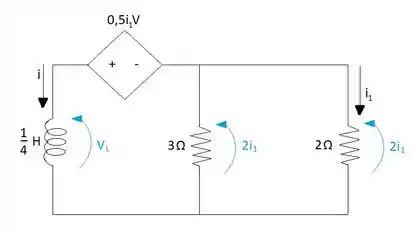
Com o desenho das polaridades no circuito é possível notar que as tensões dos resistores é a mesma, já que estão associados em paralelo, logo, é possível calcular o valor dessa tensão. No entanto, não se tem o valor da corrente eu passa por nenhum dos dois resistores, então se procura relacionar essas tensões:
Essa corrente é a corrente que passa pelo resistor de 3 Ω e dessa forma obtemos os valores das correntes em termos de , que fica da seguinte forma:
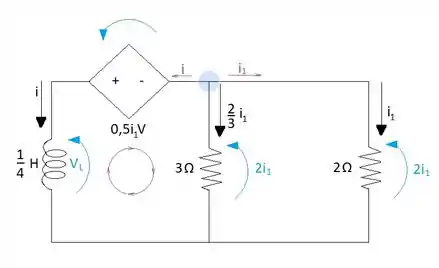
Agora só falta aplicar no nó superior a LKC para encontrar o valor da tensão do resistor de 3 Ω em termos de i:
Passo 2
Com os dados encontrados é possível dar continuidade à resolução da questão aplicando a LKT usando o ponto indicado em laranja como início da malha, lembrando que será usado a malha do lado esquerdo, já que se quer achar a expressão de i:
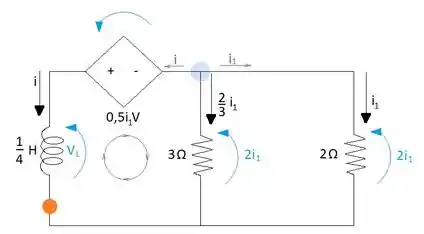
Com a substituição do valor de para deixar em termos de i:
Passo 3
Para finalizar precisamos escrever essa equação em termos de i e para isso reescrevemos ela substituindo pela sua expressão em termos de corrente:
Como se obteve uma equação diferencial, é preciso resolvê-la e considerar ainda o valor da corrente em t = 0 que foi dado no enunciado da questão. Pela resolução de uma EDO assim sabe-se que:
Dessa forma, com os dados já obtidos até o presente momento, a resposta é a seguinte: