Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 51
Em vez de aplicar a técnica reduzida usada na Seção 7.6, use a LKT para obter a Equação (7.60).
Passo 1
Certo pessoal, vamos tranquilo e entender o que a questão pede. Vamos sair um pouco da nossa zona de conforto e voltar as origens! Consideremos o circuito abaixo!
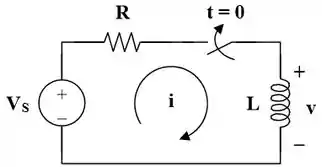
Depois que o interruptor é fechado, aplicamos a LKT e temos:
Ou,
Passo 2
Continuando com as continhas, vamos integrar dos dois lados!
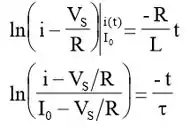
Ou,
Portanto, isolando:
Que é a equação 7.60!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine i t e v t para t0 no circuito da Figura 7.102 se i 0 = 10A .
Para o circuito da figura 7.100, v = 90 ⋅ e - 50 tV e i = 30 ⋅ e - 50 tA , t0 a Determine L e R b Determine a constante de tempo c Calcule a energia inicial no indutor. d Que fração de energia inicial
Considere o circuito da Figura 7.103. Dado que v 0 0 = 10V , determine v 0 e v x para t0 .
Para o circuito da Figura 7.80 , a corrente no indutor imediatamente antes de t = 0 é: 8A 6A 4A 2A 0A
Um circuito R L tem R = 2Ω e L = 4H . O tempo necessário para a corrente no indutor atingir 40 % de seu valor no regime estacionário é: 0,5s 1s 8s 16s Nenhuma das anteriores