Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 3

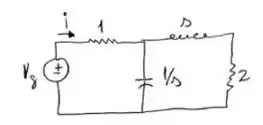
Calcule a admitância Y ( s ) vista pela fonte e coloque seus pólos e zeros. Se a fonte é v g = 4 e - t c o s ⁡ t   V , calcule a resposta forçada i

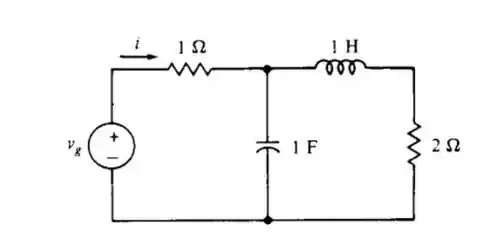
Passo 1

E aí gurizada tudo belezinha? O enunciado pede para determinamos admitância Y ( s ) , começamos trazendo um esboço do circuito :) lembrando que Em eletricidade, admitância, simbolizada Y, é o inverso da impedância. Ele é medida S (siemens).

V δ = 4 e - t c o s ⁡ t

s = - 1 + j                         V s = 4 ∠ 0 °

Z ( s ) = 1 + 1 / s ( 2 + s ) 1 / s + 2 + s = 1 + 1 / s ( 2 + s ) 1 + 2 s + s 2 s ⇒ 1 + 2 + s s 2 + 2 s + 1

Z ( s ) = s 2 + 2 s + 1 + 2 + s s 2 + 2 s + 1 = s 2 + 3 s + 3 s 2 + 2 s + 1

y ( s ) = s 2 + 2 s + 1 s 2 + 3 s + 3

Passo 2

i = V ( s ) ⋅ Y ( s ) = 4 ⋅ ( - 1 + j ) 2 + 2 ( - 1 + j ) + 1 ( - 1 + j ) 2 + 3 ( - 4 + j ) + 3 = 4 j ⇒

i = 4 ∠ 90 ∘

i = 4 e - t c o s ⁡ t + 90 ∘ = 4 e - t s e n ⁡ t A

Resposta

i = 4 e - t c o s ⁡ t + 90 ∘ = 4 e - t s e n ⁡ t A

Exercícios de Livros Relacionados

Para o circuito RLC paralelo em ressonância, mostre que a energia total armazenada é w t = 1 2 R 2 C I M 2 cos 2 ⁡ w 0 t + R 2 I M 2 2 w 0 2 L sin 2 ⁡ w 0 L = 1 2 R 2 C I M 2 Onde a excitação é i = I
No Ex. 14.4.3, substitua 0 resistor de 8Ω por 2Ω , mostre que o circuito e um filtro passa-faixa e caIcule w oeQ .
Para o circuito RLC serie com excitação v g = v m cos ⁡ w tV , mostre que w 0 = 1 L C e Q = w 0 L R . A resposta é corrente de laço.
Use o método desta seção para esboçar as respostas em amplitude e em fase H s = 16 s s 2 + 4 s + 2504
Altere em escala a frequência e a impedância do circuito da Fig. 15.4 para obter w c = 2000 π r a d s( f c = 1000H z ) usando capacitores de 0,01e0,005μ F .