Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.6 - Ex. 3
Calcule para se o circuito está em regime permanente cc em .
Passo 1
Olá pessoal, aqui é o Corazon do RespondeAí. Irei ajudar vocês nesta questão de elétrica, vamos lá.
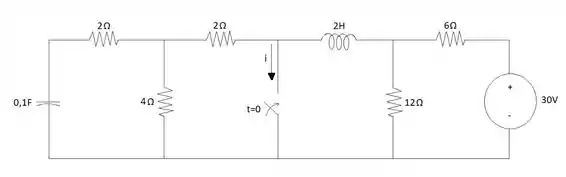
Temos que encontrar a expressão da corrente indicada na figura para e o que sabemos é que para o circuito se encontra em regime permanente. Se analisarmos o circuito com a chave aberta em regime permanente substituímos o indutor por um curto-circuito e o capacitor por um circuito aberto, ficando desse jeito:
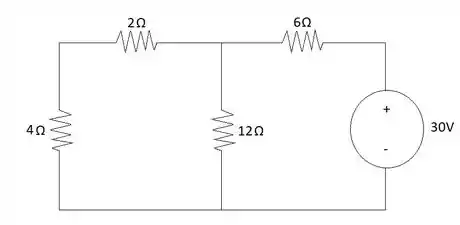
Pelo fato de a chave estar aberta, não passa corrente por essa parte do circuito, então podemos concluir que para temos .
Passo 2
Após realizar a análise anterior podemos prosseguir para a análise do circuito para . Com a chave fechada ocorre um curto circuito nessa parte o que faz com que se originem dois circuitos independentes que devem ser analisados separadamente e a corrente que passa pela chave será a soma dessas contribuições das correntes visto que o sentido de ambas correntes é o mesmo. O circuito com a chave fechada fica da seguinte forma:
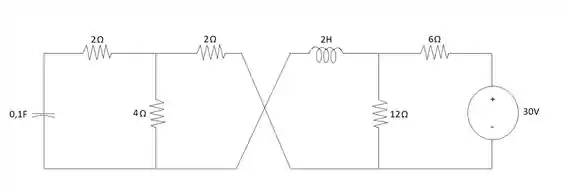
Primeiro iremos analisar o circuito onde está presente o capacitor começando com a sua resposta forçada da corrente. Entretanto, quando colocamos esse circuito em regime permanente vemos que não há passagem de corrente elétrica devido ao fato do capacitor ser substituído por um circuito aberto e então não há mais um gerador de eletricidade. Então para esse circuito temos:
Quando passamos para a análise da resposta natural devemos calcular a constante do tempo e para isso precisamos da resistência equivalente vista pelo capacitor.
Com isso podemos escrever a resposta natural da seguinte forma:
Agora só precisamos juntar as respostas natural e forçada e encontrar a constante A usando o valor de .
Substituindo na expressão anterior temos:
Isso quer dizer que não há contribuição dessa parte do circuito na corrente que estamos procurando.
Passo 3
Agora vamos descobrir as respostas forçada e natural do circuito que tem o indutor. Primeiro vamos encontrar a resposta forçada do circuito, ou seja, devemos coloca-lo em regime permanente. Em regime permanente esse circuito realiza um curto-circuito no resistor de 2 Ω então a corrente que passa pela chave é:
Com o valor da resposta forçada encontrada podemos prosseguir para o cálculo da resposta natural. No caso da resposta natural precisamos encontrar a constante de tempo e para isso devemos substituir a fonte de tensão por um curto-circuito e calcular a resistência equivalente vista pelo indutor.
Assim a resposta natural fica:
Com isso podemos escrever a resposta completa do circuito do indutor:
Usando o valor de encontramos o valor da constante A:
Substituindo na resposta do circuito do indutor:
Passo 4
Para a resposta final precisamos somar as duas contribuímos de correntes que passam pela chave, mas como não há contribuição pelo circuito do capacitor a resposta fica: