Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 79

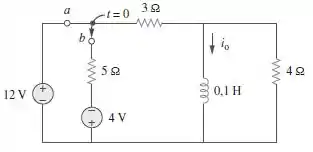
No circuito da Figura 7.143, a chave já se encontra na posição a há um bom tempo, porém, muda de repente para a posição b em t = 0. Determine (t).

Passo 1

Primeiro vamos analisar o circuito para a chave na posição (a).

Observe que ele não sofre influência da fonte de 4 V, somente da fonte de 12V, como também por se encontrar há um bom tempo nesta posição podemos substituir o indutor por um curto circuito.

Desse modo, sobra somente uma fonte de 12 V com um resistor de 3. Assim

Passo 2

Para a chave na posição 2 temos que a fonte de 12 V não tem influência no circuito, somente a fonte de 4 V.

Certo! Agora precisamos achar a resistência de Thévenin que é vista pelo indutor, ou seja, temos que curto circuitar a fonte de 4 V e tirar o equivalente da resistência vista pelo indutor. Assim,

Logo, a constante de tempo é

Passo 3

Próximo passo é tender o tempo ao infinito e analisar o circuito, desse modo substituímos o indutor por um curto circuito, e calculamos a corrente.

Atente-se para o sentido da corrente, desse modo,

Substituindo em,

Temos,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V

Se v_s mudar de 2 V para 4 V em t = 0 , podemos expressar v_s como:(a) delta (t) V (b) 2 u (t) V (c) 2 u (- t) + 4 u (t) V (d) 2 + 2 u (t) V (e) 4 u (t) - 2 V

No circuito da figura 7.80, i (oo) é:(a) 10 A (b) 6 A (c) 4 A (d) 2 A (e) 0 A

A constante de tempo para um circuito R L com R = 2 Ω e L = 4 H é:(a) 0,5 s (b) 2 s (c) 4 s (d) 8 s (e) 15 s

Para o circuito da figura 7.91, determine i_0 para t = 0 .