Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.6 - Ex. 2

Calcule v e i para t > 0 , se seu circuito está em regime permanente cc em t = 0 - .

Passo 1

Olá meus amigos! O RespondeAí irá ajudar vocês em mais uma questão, vamos lá!

Esta questão apresenta um circuito aparentemente difícil de resolver, mas ele não é tão difícil, basta apenas analisa-lo com calma e passo a passo.

Primeiro precisamos analisar o circuito em t = 0 - para poder encontrar a expressão da tensão e da corrente em t > 0 . Pelos dados que o enunciado nos fornece sabemos que no tempo t = 0 - o circuito se encontra em regime permanente, logo o indutor é substituído por um curto-circuito e isso facilita ainda mais a análise do circuito.

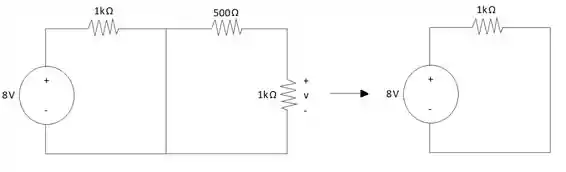
Com o circuito simplificado podemos realizar os cálculos de v 0 - e i 0 - . Devido ao curto circuito provocado pelo indutor temos que v 0 - = 0 e a corrente será:

i 0 - = 8   V 1000   Ω = 8   m A

Passo 2

Após a análise do circuito em t = 0 - devemos analisar o circuito em t > 0 e encontrar a resposta no formato de:

i = i n + i f

Sendo assim, começaremos a análise da resposta forçada do circuito para a corrente e para a tensão desejada. O circuito em t > 0 fica da seguinte forma:

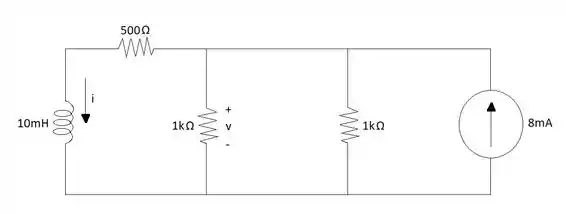
Para encontrar a resposta forçada da corrente basta realizar curto circuito no indutor e a corrente que passar pelo resistor de 500   Ω será a mesma corrente que passa pelo indutor.

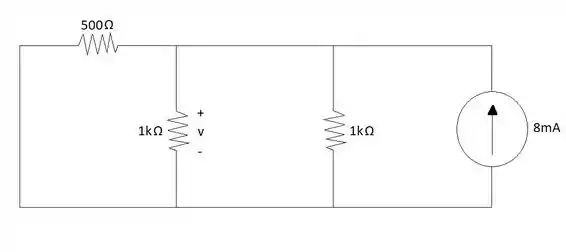
Pelos cálculos teremos o seguinte:

R e q = 500   Ω   .   1000   Ω 500   Ω + 1000 Ω = 333,33   Ω

i 1 = 8 . 10 - 3   A 1000   Ω 1000   Ω + 333,33   Ω = 6   m A

i f = 6 . 10 - 3   A 1000   Ω 1000   Ω + 500   Ω = 4   m A

Visto que o circuito todo está em paralelo, podemos dizer que tensão de todos os resistores são iguais, e resolvendo pela resistência equivalente teremos a seguinte tensão:

v f = 333,33   Ω   .   8   m A = 2   V

Passo 3

Com os cálculos das respostas forçadas podemos dar continuidade com o cálculo da resposta natural da corrente e da tensão. Desta vez substituímos a fonte de corrente por um circuito aberto e damos continuidade aos cálculos.

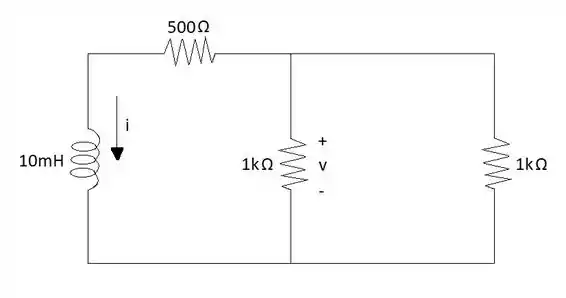
Precisamos encontrar a constante de tempo e para isso devemos calcular o valor da resistência equivalente do circuito sem a fonte de corrente:

R e q = 500   Ω + 1000   Ω   .   1000   Ω 1000   Ω + 1000 Ω = 1000   Ω

T = L R = 10   m H 1000   Ω = 10 5   s

Com o valor da constante de tempo podemos escrever a resposta natural da corrente:

i n = A e - 10 5 t

Agora iremos calcular a resposta natural da tensão:

v n = A e - 10 5 t

Passo 4

Agora que temos as respostas natural e forçada da tensão e da corrente, falta apenas encontrar o valor da constante que aparece em cada um. Para isso escreveremos a resposta completa de cada um e usaremos os valores de i 0 - e v 0 - para encontrar o valor da constante.

Para a corrente temos o seguinte:

i ( t ) = A e - 10 5 t + 4

8   m A = A + 4   m A

A = 4   m A

Substituindo:

i t = 4 e - 10 5 t + 4   m A

Para a tensão temos o seguinte:

v ( t ) = A e - 10 5 t + 2

0 = A + 2

A = - 2   V

Substituindo:

v t = - 2 e - 10 5 t + 2   V

E é isso galera, problema resolvido.

Resposta

i t = 4 1 + e - 10 5 t   m A

v t = 2 1 - e - 10 5 t   V

Exercícios de Livros Relacionados

No circuito da figura 7.10, determine o valor de R para o qual a energia em regime estacionário armazenada no indutor seja 1 J .
No circuito da figura 7.93, v t = 80 ⋅ e - 10 3 tV , t0 i t = 5 ⋅ e - 10 3 tm A , t0 a Determine R , Leτ . b Calcule a energia dissipada na resistência para 0t0.5 m s .
Determine a constante de tempo para cada um dos circuitos da figura 7.95.
Considere o circuito da Figura 7.97. Determine v 0 t se i 0 = 6 A e v t = 0 .
Determine i t e v t para t0 no circuito da Figura 7.102 se i 0 = 10A .