Resolva o Ex. 8.5.1 usando o procedimento simplificado desta seção.
Passo 1
Olá amigos! Tudo bem com vocês? Vamos resolver esta questão.
Como se trata de uma questão que já foi resolvida anteriormente já sabemos a resposta dela, mas precisamos chegar à mesma resposta usando o método desta seção, então vamos lá.
De acordo com o método de resolução desta seção a resposta aparece da seguinte forma:
Sendo que representa a resposta natural no formato de e é constante.
Para resolver usando este método iremos analisar primeiro somente da forma natural, mas faremos isso para calcular a corrente, visto que temos como um dado do enunciado, para depois calcular a tensão, que é o que a questão pede. Para encontrar a resposta natural da corrente substituímos a fonte de tensão por um curto-circuito e calculamos a constante de tempo e aplicamos na fórmula da resposta natural.
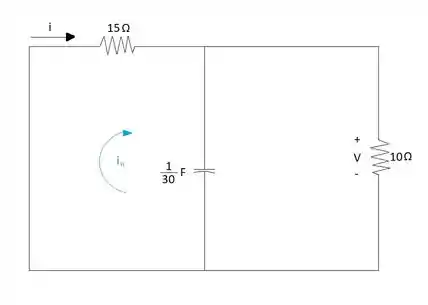
Para encontrar o valor da constante A que aparece na expressão devemos usar o valor de :
Assim a expressão fica da seguinte forma:
Passo 2
Depois de calcular a resposta natural damos continuidade calculando a resposta forçada, e como ela é forçada não importa em que tempo olhamos para o circuito, então para a resposta forçada consideramos o circuito em regime permanente.
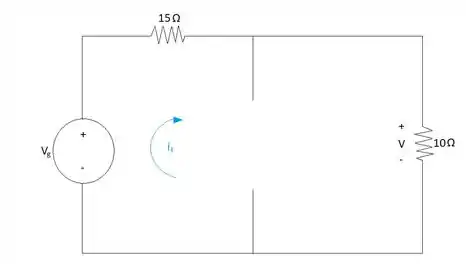
Passo 3
Com as duas respostas da corrente podemos continuar para o cálculo da tensão que queremos. Para a resposta forçada da tensão é só usar o circuito em regime permanente e calcular a tensão forçada usando a corrente forçada no resistor de 10 Ω:
Já para a resposta natural precisamos fazer uma divisor de corrente, pois usaremos o circuito sem a fonte de tensão, e aí encontraremos a corrente que sai do capacitor:
Passo 4
Com o valor da corrente que sai do capacitor agora só é preciso calcular a quantidade de corrente que vai para o resistor de 10 Ω:
Agora só calculamos a tensão do resistor de 10 Ω usando a corrente que passa por ele:
Com isso só devemos escrever a resposta de acordo como método usando o valor de resposta natural e o valor de resposta forçada.