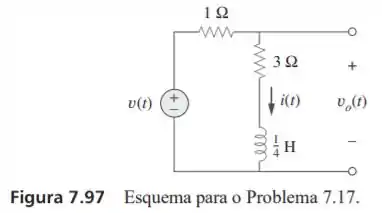
Considere o circuito da Figura 7.97. Determine se e .
Passo 1
Para esse problema vamos primeiramente encontrar a expressão para visto que foi dada condição iniciada relacionada à mesma. Nossa expressão para terá o formato
Onde . Mas como encontramos o valor da resistência equivalente ? Vamos encontrar a resistência equivalente entre os terminais do indutor, para isso vamos substituir a fonte de tensão por um curto – circuito:
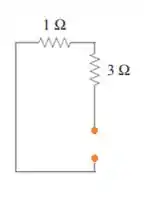
Ou seja, as resistências estão em série:
Logo, a constante de tempo :
Então
Passo 2
Pronto, agora temos tudo o que precisamos para encontrar o valor de fazendo
Onde
Portanto,
Nesse caso, a função degrau indica que a análise começa somente a partir do instante de tempo . E pronto, está finalizado nosso exercício.