Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 5
Usando a figura 7.85, elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos sem fontes.
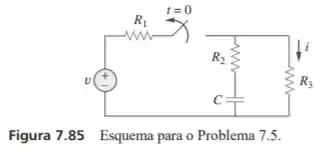
Passo 1
Se denominarmos a tensão que passa pelo capacitor podemos encontrar pela observação do circuito que em podemos aplicar o divisor de tensão e assim teremos
Para temos um circuito sem fonte, ou seja, só precisaremos considerar a malha da direita do nosso circuito original. Assim, podemos encontrar nossa constante de tempo fazendo
Sendo assim, conseguimos equacionar obtendo assim
Por fim, devemos nos lembrar que o capacitor possui a seguinte a equação
Aplicando os dados obtidos anteriormente vamos encontrar
Resposta
Exercícios de Livros Relacionados
A chave do circuito mostrado na Figura P7.60 abre em t = 0 depois de estar fechada por um longo tempo. Em quantos milissegundos, depois de a chave estar aberta, a energia armazenada no capacitor ating
a) A chave no circuito da Figura P7.52 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b e permanece lá. Determine os valores inicial e final da tensão do c
A chave no circuito da Figura P7.53 esteve na posição a por um longo tempo. Em t = 0, ela é colocada na posição b. Calcule (a) a tensão inicial no capacitor; (b) a tensão final no capacitor; (c) a con
A chave no circuito visto na Figura P7.54 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Para t $ 0+, determine a) vo (t). b) i o (t).
A chave do circuito visto na Figura P7.55 esteve na posição a por um longo tempo. Em t = 0, a chave passa instantaneamente para a posição b. Determine vo (t) e i o (t) para t $ 0+.