Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 34
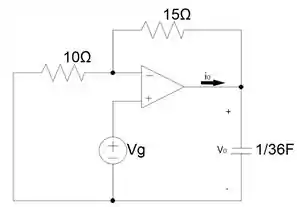
Calcule, para , a corrente que entra para baixo no capacitor, se , e (a) , (b) , e (c) .
Passo 1
Iae, meus queridos, td belezinha??
Você pode achar essa questão um pouco trabalhosa, mas nada é difícil pra quem é estudioso como você. 😉
A questão nos disse que , isso significa que o capacitor está completamente descarregado em .
Para cada item, vamos utilizar o seguinte passo a passo:
Notamos que o amplificador no circuito é do tipo Não-Inversor, portanto vamos utilizar aquela formulinha simples para calcular a tensão de saída do Amp Op:
Após essa parte, vamos partir pra calcular , aplicando a Lei de Ohm. Em seguida calcular visto pelo capacitor.
Substituir os dados encontrados na função para circuitos RC com fonte.
E por fim, aplicar a função com a função encontrada anteriormente.
Então, mão na massa!
Passo 2
(a)
Primeiro a tenção de saída .
Calculando .
Aplicando a Lei de Ohm para encontrar visto pela fonte.
Substituindo em .
Por fim, derivar e multiplicar por .
Passo 3
(b)
Primeiro a tenção de saída .
Calculando .
Aplicando a Lei de Ohm para encontrar visto pela fonte.
Substituindo em .
Por fim, derivar e multiplicar por .
Passo 4
(c)
Primeiro a tenção de saída .
Calculando .
Aplicando a Lei de Ohm para encontrar visto pela fonte.
Substituindo em .
Por fim, derivar e multiplicar por .
Resposta
a)
b)
c)