Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.9 - Ex. 4

Verifique que 0 circuito da Fig. 14.22 e equivalente a rede genérica de três terminais, mostrando que (14.41) se aplica.

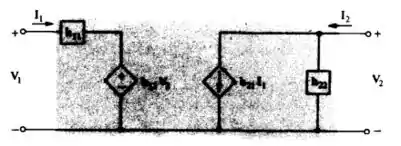
Passo 1

Nessa questão ele pede para verificar o que o circuito

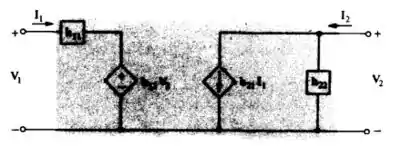
É equivalente à rede genérica de três terminais mostrando que,

v 1 = h 11 I 1 + h 12 V 2

I 2 = h 21 I 1 + h 22 V 2

Se aplica

Fica assustado não que você vai ver que é de boa.

Passo 2

Sabendo que,

v 1 = h 11 I 1 + h 12 V 2

I 2 = h 21 I 1 + h 22 V 2

h 11 = v 1 I 1 ​ v 2 = 0   h 12 = v 1 v 2 ​ I 1 = 0

h 21 = I 2 I 1 ​ v 2 = 0 h 22 = I 2 v 2 ​ I 1 = 0

Para,

Z i n = v g I 1 = Z 11 + Z g - Z 12 Z 21 Z 22 + Z L

Assim ela se aplica.

Espero ter ajudado, bons estudos e até a próxima.

Resposta

Z i n = v g I 1 = Z 11 + Z g - Z 12 Z 21 Z 22 + Z L

Assim ela se aplica.

Exercícios de Livros Relacionados

a) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor, um indutor e um capacitor em série para criar uma impedância de 300 - j400 Ω a uma frequência de 10.000 rad/s. b)
Determine a admitância Y a b no circuito visto na Figura P9.23. Expresse Y a b em forma polar e também em forma retangular. Determine o valor de Y a b em milissiemens.
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = R 2 1 + ω 2 R 2 2 C 2 2 C 1 = 1 + ω 2 R 2 2 C 2 2 ω 2 R 2 2 C 2
a) Usando os valores dos componentes do apêndice H, determine um único capacitor ou uma rede de capacitores que, quando combinados em paralelo com o circuito RL do Problema 9.26(a), resulta em uma imp
a) Para o circuito mostrado na Figura P9.24, determine a frequência (em radianos por segundo) em que a impedância Z a b é puramente resistiva. b) Determine o valor de Z a b na frequência determinada n