Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.1 - Ex. 1

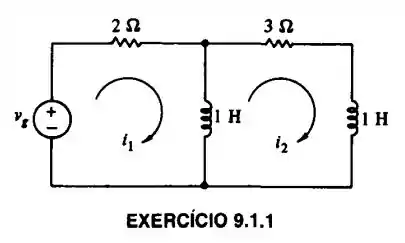
Calcule a equação que satisfaz a corrente de malha i 2

Passo 1

Bom, para começarmos a resolver esse circuito, vamos aplicar a Lei das Malhas e então vamos deixar i 2 em evidência para termos uma equação apenas com i 2 .

Aplicando a LKT na primeira malha, teremos:

2 i 1 + 1 d i 1 d t - 1 d i 2 d t = v g

2 i 1 + d i 1 d t - d i 2 d t = v g

Agora, aplicando a LKT na segunda malha, teremos:

3 i 2 + 1 d i 2 d t + 1 d i 2 d t - 1 d i 1 d t = 0

3 i 2 + 2 d i 2 d t - d i 1 d t = 0

Passo 2

Da equação da primeira malha, podemos diferenciá-la para obtermos:

2 d i 1 d t + d 2 i 1 d t 2 - d 2 i 2 d t 2 = d v g d t

Agora vamos encontrar os valores de d i 1 / d t e d 2 i 1 / d t 2 , usando a equação da segunda malha:

Para encontrar a primeira derivada, é só colocar d i 1 d t em evidência:

d i 1 d t = 3 i 2 + 2 d i 2 d t

E para encontrar a segunda derivada, devemos diferenciar essa equação:

d 2 i 1 d t 2 = 3 d i 2 d t + 2 d 2 i 2 d t 2

Agora substituímos essas equações, na equação da primeira malha.

Passo 3

Substituindo, teremos:

2 d i 1 d t + d 2 i 1 d t 2 - d 2 i 2 d t 2 = d v g d t

2 3 i 2 + 2 d i 2 d t + 3 d i 2 d t + 2 d 2 i 2 d t 2 - d 2 i 2 d t 2 = d v g d t

Organizando os termos:

6 i 2 + 4 d i 2 d t + 3 d i 2 d t + 2 d 2 i 2 d t 2 - d 2 i 2 d t 2 = d v g d t

6 i 2 + 7 d i 2 d t + d 2 i 2 d t 2 = d v g d t

E colocando as derivadas de ordem superior na frente, pra ficar bonito:

d 2 i 2 d t 2 + 7 d i 2 d t + 6 i 2 = d v g d t

Resposta

d 2 i 2 d t 2 + 7 d i 2 d t + 6 i 2 = d v g d t

Exercícios de Livros Relacionados

Determine o dual do circuito da Figura 8.120 .
Obtenha o dual do circuito da Figura 8.119 .
Desenhe o dual do circuito da Figura 8.12 1 .
O modelo de uma carga é um indutor de 250m H em paralelo a um resistor de 12Ω . É preciso que um capacitor esteja conectado à carga de modo que o circuito apresente amortecimento crítico para a frequê
Um acionador de airbag para automóvel é modelado pelo circuito mostrado na Figura 8.122 . Determine o tempo necessário para a tensão no acionador atingir seu primeiro pico após mudar da posição A para