Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 78
Um acionador de airbag para automóvel é modelado pelo circuito mostrado na Figura . Determine o tempo necessário para a tensão no acionador atingir seu primeiro pico após mudar da posição para . Seja e .
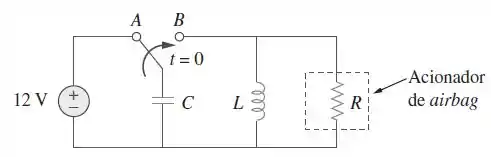
Passo 1
Pessoal, vamos dividir a solução em dois momentos aqui. Quando , a chave está na posição e as condições do regime permanentes são válidas. O capacitor se comporta como um circuito aberto nos levando a concluir que
Além disso, a corrente que passa tanto pelo indutor quanto pelo resistor em são iguais a:
Passo 2
Quando , a chave troca para a posição , criando um circuito paralelo. Podemos aqui encontrar os valores para e , a fim de encontrarmos a solução.
Como , nosso circuito é subamortecido e a frequência de amortecimento é dada por:
Passo 3
A tensão pode ser escrita como:
Para ,
Do nosso circuito resultante quando , vamos aplicar a lei dos nós no nó do indutor quando :
Porém,
Passo 4
Se derivarmos a equação ,
Quando ,
Substituindo e em :
Para encontrarmos o pico, basta derivarmos e igualarmos a zero:
Aplicando a função inversa da tangente, temos:
Resposta
O tempo é igual a: