Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 40

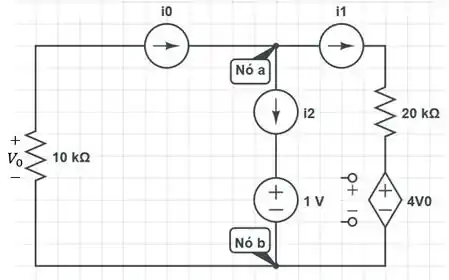
40. Determine o equivalente de T h é v e n i n   nos terminais a - b do circuito da Figura 4.107

Passo 1

Bom! O raciocínio dessa questão, é um pouco diferente do que a gente vinha fazendo.

Sabe porque? Dessa vez, vamos nos concentrar em obter primeira, a tensão equivalente de T h é v e n i n , V T h .

E para fazer isso, vamos aplicar a lei das tensões de K i r c h h o f f nesse nosso circuito:

- 70 + 10000 i + 20000 i + 4 V 0 = 0

Só que da figura do enunciado, podemos ver claramente que:

V 0 = 10000 i

O que nos leva à:

- 70 + 10000 i + 20000 i + 4 ⋅ ( 10000 i ) = 0

70000 i = 70

i = 70 70000   A

i = 1   m A

Passo 2

Com isso, para obter a tensão V T h , basta aplicar a lei das tensões de K i r c h h o f f para qualquer uma das duas malhas desse nosso circuito. Tomemos a 1 ° malha...

- 70 + 10000 i + V T h = 0

- 70 + 10000 ⋅ 0,001 + V T h = 0

V T h = 60   V

Passo 3

Tamo indo bem! Para encontrar a resistência de T h é v e n i n , bora fazer algumas alterações no nosso circuito, excluindo a fonte de tensão de 70   V . De modo que ele vai ficar do seguinte jeito:

E em seguida, bora aplicar a lei das tensões de K i r c h h o f f para essa malha à direita.

- 1 + 20000 i 2 + 4 V 0 = 0

Só que V 0 é o produto da resistência de 10   k Ω pela corrente i obtida anteriormente, de 1   m A . Sendo assim:

Mas iremos adotar V o = - 1   V

- 1 + 20000 i 1 + 4 V 0 = 0

- 1 + 20000 i 1 + 4 ( - 1 i ) = 0

- 1 + 20000 i 1 - 4 = 0

20000 i 1 = 5

i 1 = 0.25   m A

Pela lei das correntes de K i r c h h o f f no nó a , podemos ver que:

i 0 = i 1 + i 2

i 2 = i 1 + 1 V 10 k

i 2 = 0.35 m A

O fato de encontrarmos uma corrente negativa, quer dizer que ela está em um sentido oposto ao que adotamos em nosso esboço

Por fim, temos que a resistência de T h é v e n i n , R T h , é dada por:

R T h = 1   V 0.35 k Ω

R T h = 2.857   k Ω

Resposta

V T h = 60   V

R T h = 2.857   k Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um voltímetro com uma resistência de 85,5 kV é usado para medir a tensão V a b no circuito da Figura P4.72.a) Qual é a leitura do voltímetro?b) Qual será a percentagem de erro na leitura do voltímetro
Obtenha o equivalente de Thévenin em relação aos terminais a, b do circuito da Figura P4.80.
Qual percentagem da potência total gerada no circuito da Figura P4.82 é fornecida a R 0 quando R 0 é ajustado para a máxima transferência de potência?
a) Obtenha o equivalente de Thévenin em relação aos terminais a, b do circuito da Figura P4.78 determinando a tensão de circuito aberto e a corrente de curto-circuito.b) Determine a resistência de Thé
O resistor variável no circuito da Figura P4.82 é ajustado para a máxima transferência de potência a R 0 .a) Determine o valor de R 0 .b) Determine a potência máxima que pode ser transferida para R 0