Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 38
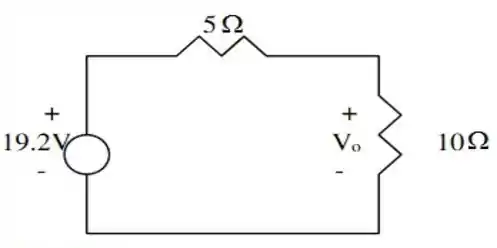
38. Aplique o teorema de para determinar no circuito da figura
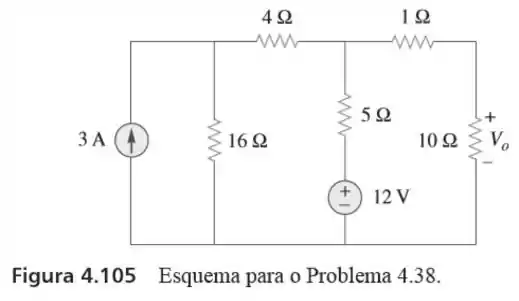
Passo 1
Bom! A primeira coisa que temos que fazer, e encontrar a resistência equivalente nos terminais do resistor de . Por isso, vamos redesenhar esse circuito do seguinte jeito:
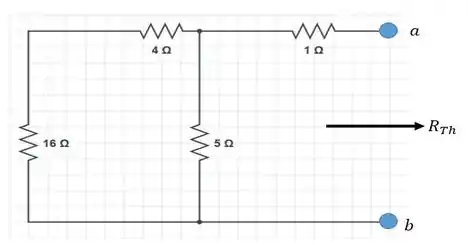
Repara que nós cortamos a resistência de .
Bora agora obter a resistência equivalente entre e , que é a nossa resistência de , .
E olhando a figura que nós fizemos, podemos ver que:
Passo 2
Em seguida, o próximo passo é obter a tensão de , .
Para isso, a primeira coisa a se fazer é excluir aquela resistência de . Já já eu explico, o porquê devemos fazer isso. Mas primeiro, vamos ao desenho do circuito sem essa resistência:
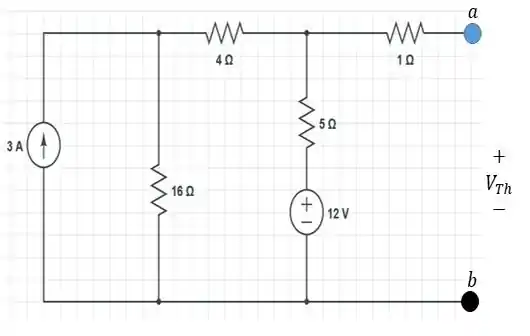
Olha só! Como nosso circuito foi aberto, nenhuma corrente irá circular naquele resistor de .
Fazendo a análise nodal, vamos entender isso de um jeito um pouco melhor.
Por esse motivo, vamos redesenhar esse circuito, dando nomes aos bois. Isto é, temos que indicar sentidos para as correntes e destacar os nós desse circuito. Vamos por a mão na massa!
Passo 3
Nosso circuito passa a ter então, a seguinte cara:
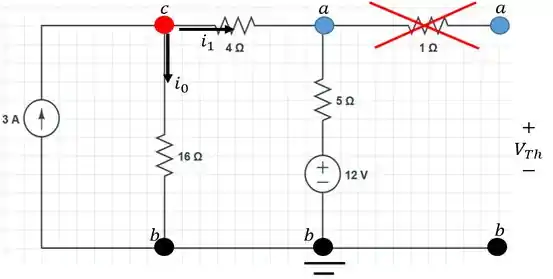
Agora as coisas estão começando a ficar mais claras. Não disse que a análise nodal ia ajudar muito!
Através dela, podemos ver claramente que a tensão de tensão de , , é dada pela diferença entre a tensão nos nós e ...
E de cara, já podemos ver que o nó é o terra. Sendo assim...
Bora então, determinar as equações de corrente para o nó usando a lei de :
Onde:
Lembrando que não circula corrente pelo resistor de , hein!?
Passo 4
Chegamos assim, até a seguinte equação:
Mas nós queremos é ! Calma calma! Não criemos pânico! é dada por:
A nossa tensão de , portanto, vai valer:
Passo 5
Como já temos a tensão e a resistência de , chegamos ao seguinte circuito:
E o valor de , pode ser facilmente obtido através da divisão de voltagem: