Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 39
39. Obtenha o equivalente de nos terminais do circuito da Figura
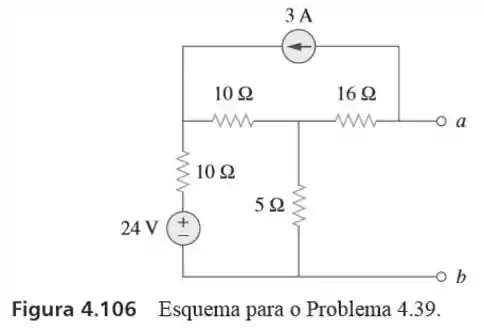
Passo 1
Bom! A primeira coisa que temos que fazer, e encontrar a resistência equivalente nos terminais . Por isso, vamos ter que redesenhar esse circuito, excluindo aquela fonte de tensão, de .
E aqui está:
Bora então, obter a resistência equivalente entre e , que é a nossa resistência de , .
E olhando a figura anterior, podemos ver que:
Passo 2
Em seguida, o próximo passo é obter a tensão de , .
Para isso, vamos ter usar a análise nodal no nosso circuito.
Podemos ver que nosso circuito tem nós... Sendo que o nó inferior, indicado por , é o que iremos adotar pra ser o nosso terra. Ou seja, quer dizer que a tensão nodal em é .
Bora então, fazer o esboço desse circuito indicando as correntes que circulam em cada ramo, bem como nomeando os nós nele presente.
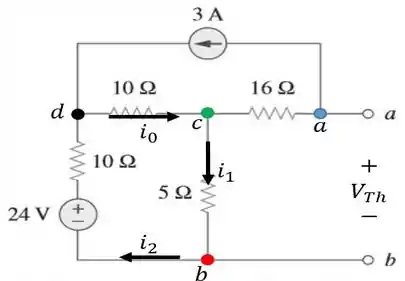
Através dessa imagem, podemos ver claramente que a tensão de tensão de , , é dada pela diferença entre a tensão nos nós e ...
Só que...
Bora então, determinar as equações de corrente para os nó e , usando a lei de :
Onde:
Passo 3
Subsituindo esses valores anteriores, nas relações que obtivemos anteriormente....
Chegamos assim, até ao seguinte sistema de equações:
Mutiplicamos por e depois somamos com a equação ... Conseguimos que:
E o valor de é dado por:
Mas nós queremos é ! Calma calma! Não criemos pânico! O valor de é dada por:
A nossa tensão de , portanto, vai valer:
Pronto! Já obtemos nossas respostas!