Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 35

Calcule a potência ativa, a potência reativa e a potência complexa entregue pela fonte.

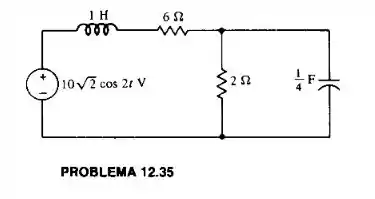
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Vamos calcular a impedância equivalente, que será igual a

Z e q = 6 + 2 j + 2 ∙ ( - 2 j ) 2 - 2 j = 7 + j = 7,07 ∠ 8,13 °  

A corrente eficaz é dada por

I e f = V e f Z e q

Substituindo os valores, nós temos que

I e f = 10 7,07 ∠ 8,13 ° = 1,414 ∠ 8,13 °

E o conjugado será igual

I e f * = 1,414 ∠ 8,13 °  

Passo 2

Logo, a potência complexa é igual a

S = V e f I e f *

Substituindo os valores, nós obtemos o seguinte resultado

S = 10 ∙ 1,414 ∠ 8,13 ° = 14,14 ∠ 8,13 °   V A

A potência ativa logo será igual a

P = 14,14 cos ⁡ ( 8,13 ° ) = 14   [ W ]

E a reativa

Q = 14,14 sin ⁡ 8,13 ° = 2   V A r

Podemos escrever S da seguinte forma

S = 14 + 2 j   [ V A ]

Resposta

S =   14,14 ∠ 8,13 °   V A

P = 14   W

Q = 2   [ V A r ]

Exercícios de Livros Relacionados

As duas cargas mostradas na Figura P10.22 podem ser descritas da seguinte forma: a carga 1 absorve uma potência média de 10 kW e uma potência reativa de 4 kVAR; a carga 2 tem uma impedância de (60 + j
Suponha que o circuito da Figura P10.24 represente um circuito de distribuição residencial no qual as impedâncias dos condutores são desprezíveis e Vg1 = Vg2 = 110/0° V (ef). As três cargas no circuit
a) Determine VL (ef) e θ para o circuito da Figura P10.19, se a carga absorver 2.500 VA, com um fator de potência atrasado de 0,8. b) Construa um diagrama fasorial de cada solução obtida em (a).
Os valores dos parâmetros do circuito da Figura P10.56 são L 1 = 8m H ; L 2 = 2m H ; k = 0,75 ; R g = 1Ω e R L = 7Ω . Se v g = 54 2 cos ⁡ 1000 tV , determinea) o valor eficaz de v o ;b) a potência méd