Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 56
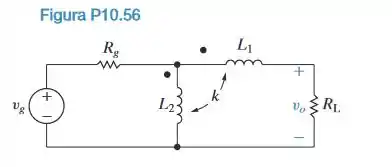
Os valores dos parâmetros do circuito da Figura P10.56 são ; ; ; e . Se , determine
a) o valor eficaz de ;
b) a potência média fornecida a ;
c) a percentagem da potência média gerada pela fonte de tensão ideal que é fornecida a .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Primeiro, vamos determinar a impedância do indutor de
Substituindo os valores,
Já no indutor de , temos que
Novamente, substituindo os valores
Agora, vamos para a indutância mútua
Desenvolvendo um pouco mais esse cálculo, nós temos que
Passo 2
Como mostrado no circuito, existem duas malhas para serem analisadas, então, por este motivo, vamos escrever duas equações de correntes de malha
Da equação (2), é igual a
Substituindo (3) em (1), as duas correntes de malhas são dadas por
Com isso, já podemos determinar a magnitude de
Fazendo a substituição,
Portanto,
Passo 3
B - A potência média entregue à resistência de carga P é dada por
Fazendo a substituição dos resultados
Portanto,
Passo 4
C - A potência complexa fornecida pela fonte de tensão é dada por
E substituindo os resultados, nós temos que
Que tem como resultado
A potência média fornecida pela fonte de tensão é dada por
Onde o sinal negativo indica que a energia é fornecida pela fonte. Determine a porcentagem da potência média fornecida pela fonte de tensão que é fornecida à resistência de carga
Substituindo os resultados
Portanto,