Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 30

Calcule a potência ativa, a potência reativa e a potência complexa entregue pela fonte e o elemento reativo que deve ser colocado em paralelo com a fonte para tornar o fator de potência visto pela fonte (a) 0.9 (adiantado) e (b) 0.8 (atrasado).

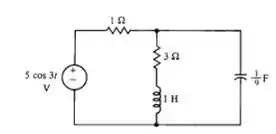
Passo 1

Calcule a potência ativa, a potência reativa e a potência complexa entregue pela fonte e o elemento reativo que deve ser colocado em paralelo com a fonte para tornar o fator de potência visto pela fonte (a) 0.9 (adiantado) e (b) 0.8 (atrasado).

ω = 3

Z e q = 1 + ( 3 + 3 j ) - 3 j 3 + 3 j - 3 j = 4 - 3 j

I = V L e g = 5 ∠ 0 5 L - 36 , 87 ∘ = 1 ∠ 36 , 87 ∘

x 1 = w L

X c = 1 ω c

P = V Rms  I Rm s   2 c o s ⁡ - 36 , 87 ∘ = 5 ⋅ 1 2 c o s ⁡ - 36 , 87 ∘ = 2 W

Q 0 = V Rms  I Rm s   2 s e n ⁡ - 36 , 87 ∘ = - 1,5 W

S = 2 - 1,5 w

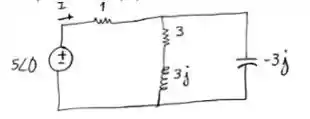
Passo 2

a. 0.9 adiantado Q T = P t g ⁡ ( ω , - 1,0 , 9 ) = 2 t g ⁡ c o s - 1 - 0,9 = - 0,97

Q x = Q T - Q 0 = - 0,97 - ( - 1,5 ) = 0,53

x 1 = V R M S 2 Q x = ( 5 / 2 ) 2 0,53 = 23,6 Ω como   x 1 > 0 é indutivo

h = x 1 a = 23,6 5 = 4,72 N

Passo 3

b. Q T = 2 tg ⁡ cos - 1 ⁡ 0,8 = 1,5

Q t = Q T - Q 0 = 1,5 - ( 1,5 ) = 3

X 1 = V RnS  2 Q x = 25 / 2 3 = 25 6 Ω

L = x 1 ω = 2 S / 6 S = 5 6 H

Resposta

a. 4,72N

b. 5 6 H

Exercícios de Livros Relacionados

Calcule o fator de potência para (a) uma carga consistindo em uma associação em série de um resistor de 10-Ω e um indutor de 10-mH operando em 60Hz, (b) uma carga capacitiva que consome 25A (eficazes)
Calcule a potência dissipada no resistor de 1 - Ω do circuito primário e o fator de poténcia visto pela fonte.
Use (12.22) para correção do fator de potência, visto pela fonte da Fig. 12.4 para A – 0,9 (Adiantado)B – 0,9 (Atrasado)
Duas cargas em paralelo consomem respectivamente 210 W com um fator de potência de 0,6 (adiantado) e 40 W com um fator de potência de 0,8 (atrasado). Se a tensão através da associação em paralelo é V
Urna carga e alimentada da potência complexa S = 6 + j 8 por uma fonte de tensão de 10 cos ⁡ 100 t . Calcule a capacitância que deve ser conectada em paralelo com a carga para que o fator de potência