Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 35

Calcule a potência máxima que pode ser entregue ao resistor R e o valor de R para a potência máxima no circuito do Prob 5.27.

Passo 1

Faaalaaaeeee!! Vai dizer que sua primeira impressão quando leu o enunciado foi:

Se preocupe não e vem comigo aqui haha

Seguinte... a gente sabe que:

P m á x = V T H 2 4 R T H

Em que:

  • P m á x é a potência máxima;
  • V T H é a tensão de Thévenin;
  • R T H é a resistência de Thévenin.

Obs: A maior transferência de potência para uma carga R será quando R = R T H .

Passo 2

Vamos aplicar LKT para descobrirmos a tensão de Thévenin nos dois nós selecionados:

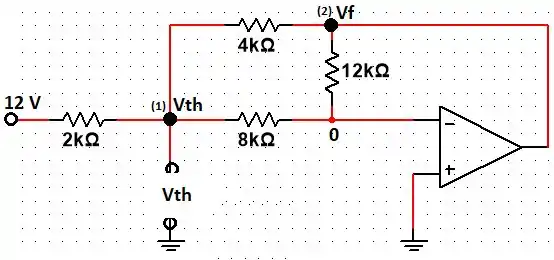
No nó 1 temos:

12 - V T H 2 k = V T H 8 k + V T H - V f 4 k

No nó 2 temos:

V T H 8 k = V f 12 k ∴ V f = 3 V T H 2

Logo, substituindo V f , temos que:

12 - V T H 2 k = 0 ∴ V T H = 12 V

Passo 3

Para descobrirmos a resistência de Thévenin R T H , percebemos que:

R T H = 2 k + 8 k | | 12 k + 4 k ∴

R T H = 22 3 k Ω = R

Passo 4

Assim, a potência máxima é dada por:

P m á x = 12 2 4 × 22 3 ∴

P m á x = 4.91 W

Tranquilo ne?? Vamos para outra!!

Resposta

R = 22 3 k Ω

P m á x = 4.91 W

Exercícios de Livros Relacionados

A tensão nos terminais de uma fonte de tensão é v = 6 ∙ s e n( 2 t )V . Se a carga que deixa o terminal positivo é q= - 2 ∙ cos ⁡ 2 tm C , calcule a potência fornecida pela fonte a qualquer tempo e a
Calcule v a b e a potência entregue pela fonte de 5 V .
Se a tensão sobre um elemento é 8V e a corrente i que entra no elemento pelo terminal positivo e a mostrada, calcule a potência entregue ao elemento em t=7m s , a carga e a energia totaisentregues ao
Se a função representada no gráfico do Prob. 1.6 e uma tensão v( v o l t s ) sobre o elemento versus o t e m p o( m s ) e a corrente que está entrando pelo terminal positivo e 2m A , calcule a potênci
A potência entregue a um elemento e p=16 e - 10 tW , a corrente i (em amperes) e positiva e a tensao e v=4 i . Calcule a tensão e a carga total entregue ao elemento para t0 .