Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.5 - Ex. 3

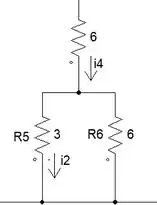
Calcule i 1 e i 2 .

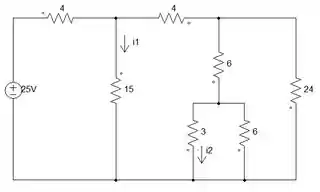
Passo 1

Antes de sabermos quanto vale i 1 e i 2 , vamos descobrir o R e q desse circuito.

O resistor de 3Ω está em paralelo com de 6Ω:

R_3 \\ \\ 6 = (3 * 6)/(3 + 6)

R_3 \\ \\ 6 = (18)/(9)

R_3 \\ \\ 6 = 2 Ω

O resistor de 2Ω está em série com o de 6Ω:

R_6 - 2 = 6 + 2

R_6 - 2 = 8 Ω

O resistor de 8Ω está em paralelo com de 24Ω:

R_8 \\ \\ 24 = (8 * 24)/(8 + 24)

R_8 \\ \\ 24 = (192)/(32)

R_8 \\ \\ 24 = 6 Ω

O resistor de 6Ω está em série com o de 4Ω:

R_6 - 4 = 6 + 4

R_6 - 4 = 10 Ω

O resistor de 10Ω está em paralelo com de 15Ω:

R_10 \\ \\ 15 = (10 * 15)/(10 + 15)

R_10 \\ \\ 15 = (150)/(25)

R_10 \\ \\ 15 = 6 Ω

O resistor de 6Ω está em série com o de 4Ω:

R_6 - 4 = 6 + 4

R_6 - 4 = 10 Ω

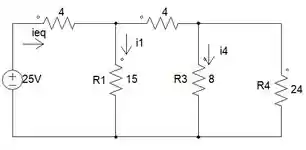
Assim fica o circuito equivalente:

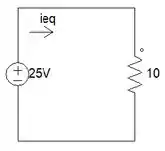
Passo 2

Agora que sabemos o circuito equivalente, podemos descobrir o i e q e posteriormente i 1 e i 2 .

Pela lei de Ohm, temos que:

V = R e q * i e q

i e q = (V)/(R e q)

i e q = (25)/(10)

i e q = 2,5 A

Para descobrir o i 1 vamos fazer divisão de corrente, pois a associação dos resistores está em paralelo.

i 1 = (R 2 * i e q)/(R 1 + R 2)

i 1 = (10 * 2,5)/(10 + 15)

i 1 = (25)/(25)

i 1 = 1 A

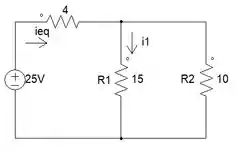
Agora, vamos fazer LKC para saber quanto de corrente está passando no resistor de 10Ω e vamos denominar de i 3 .

i e q = i 1 + i 3

i 3 = i e q - i 1

i 3 = 2,5 - 1

i 3 = 1,5 A

Vamos descobrir uma nova corrente, a que vai passar no resistor de 8Ω e iremos chamá-lo de i 4 . E, vamos usar o i 3 na divisão de corrente.

i 4 = (R 4 * i 3)/(R 4 + R 3)

i 4 = (24 * 1,5)/(24 + 8)

i 4 = (36)/(32)

i 4 = 1,125 A

Maravilha! Já sabemos a corrente que está passando no resistor de 8Ω, que é a associação dos resistores, onde encontrasse o resistor que passa o i 2 . Vamos fazer divisão de corrente mais uma vez usando o i 4 .

i 2 = (R 6 * i 4)/(R 5 + R 6)

i 2 = (6 * 1,125)/(3 + 6)

i 2 = (6,75)/(9)

i 2 = 0,75 A

Resposta

i 1 = 1 A

i 2 = 0,75 A

Exercícios de Livros Relacionados

Para cada um dos circuitos mostrados na Figura P3.4, a) determine a resistência equivalente vista pela fonte, b) determine a potência fornecida pela fonte
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Δ inferior ( 25 ; 37,5e40Ω ) por seu Y equivalente.
Mostre que as expressões para condutâncias em Δ em função das três condutâncias em Y são G a = G 2 G 3 G 1 + G 2 + G 3 G b = G 1 G 3 G 1 + G 2 + G 3 G c = G 1 G 2 G 1 + G 2 + G 3 em que G a = 1 R a ,
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Y à direita ( 25 ; 37,5e125Ω ) por seu Δ equivalente.
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Y à esquerda ( 25 ; 40e100Ω ) por seu Δ equivalente.