Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.4 - Ex. 2

Calcule H ( s ) se a resposta é (a) I_1 ( s ) , (b) I_0 ( s ) e (c) V_0 ( s ) .

Passo 1

É OQ??

Vamos com calminha!!

Sabemos que, para uma resistência R , a impedância é:

Z_R (s) = R

Para uma indutância L , sua impedância é:

Z_L (s) = s L

E, para uma capacitância C , sua impedância é:

Z_C (s) = (1)/(s C)

Nesse sentido, para o circuito desse exercício, temos:

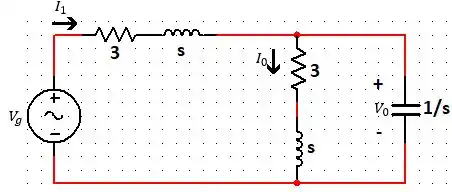
Passo 2

Sabemos que I_1 é a corrente equivalente de todo o circuito. Assim, vamos descobrir a impedância equivalente.

Z_e q = (3 + s) + [(3 + s) | | ( 1 // s )] :.

Z_e q = (3 + s) + ([(3 + s) xx ((1)/(s))])/((3 + s) + ((1)/(s))) :.

Z_e q = (3 + s) + (3 + s)/(3 s + s^2 + 1) :.

Z_e q = (s^2 + 3 s + 1)/(( s + 1 ) ( s + 2 ) ( s + 3 ))

Sabemos que:

I_1 = (V_g)/(Z_e q)

Logo, temos que:

H (s) = (1)/(Z_e q) = (( s + 1 ) ( s + 2 ) ( s + 3 ))/(s^2 + 3 s + 1)

Passo 3

Sabemos que V_0 no capacitor é igual a tensão no indutor e no resistor que estão paralelos a ele. Assim, fazemos o divisor de tensão:

V_0 = V_g (([(3 + s) ((1)/(s))])/((3 + s) + ((1)/(s))))/(([(3 + s) ((1)/(s))])/((3 + s) + ((1)/(s))) + (3 + s)) :.

V_0 = V_g (1)/((s + 1) ( s + 2 ))

Assim fica fácil perceber que:

H (s) = (1)/((s + 1) ( s + 2 ))

Passo 4

Podemos calcular I_0 de tal forma que:

I_0 = (V_0)/(s + 3)

Ou seja, substituindo V_0 , temos que:

I_0 = V_g (1)/((s + 1) ( s + 2 ) ( s + 3 ))

Que também fica bem facinho de perceber que:

H (s) = (1)/((s + 1) ( s + 2 ) ( s + 3 ))

Até que não é tão complicada né? Responde aí!!

Resposta

a) H (s) = (( s + 1 ) ( s + 2 ) ( s + 3 ))/(s^2 + 3 s + 1)

b) H (s) = (1)/((s + 1) ( s + 2 ) ( s + 3 ))

c) H (s) = (1)/((s + 1) ( s + 2 ))

Exercícios de Livros Relacionados

Mostre que os parâmetros híbridos definidos em (14.42) podem ser obtidos a partir dos parâmetros z por g 11 = 1 z 11 ,g 12 = - z 12 z 11g 21 = z 21 z 11 ,g 22 = Δ z z 11 Onde Δ Z = Z 11 Z 22 - Z 12 Z
Considerando a figura do Prob. 14.22 como um quadripolo com terminais como indicado, calcule os parâmetros z e y em função de 5 .
Calcule os parâmetros y no Prob. 14.16 .
Mostre que os parâmetros de transmissão, A , B , C e D, definidos para o quadripolo da Fig. 14.12 como V 1 = A V 2 - B I 2 I 1 = C V 2 - D I 2 São dados por A = z 11 z 21 , B = Δ Z Z 21 C = 1 z 21 , D
O circuito mostrado é uma treliça com dois braços em série iguais a Z a e dois braços em cruz iguais a Z b . Este circuito é chamado treliça simétrica porque os braços em série são iguais e os braços